在长方形中画出5条线,把它分成的块数与画线的方式有直接关系.按如图1的方式画线,可以把它分成10块.请你在图2中画出5条线,使得把这个长方形分成的块数最少(重合的线只看做一条),最少可分成 块;
请你在图2中画出5条线,使得把这个长方形分成的块数最多,最多可分成 块.
(画出图形不写画法和理由)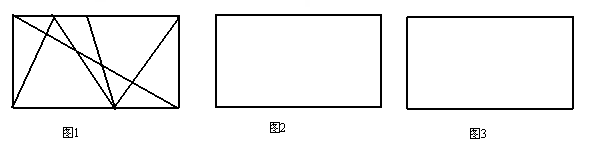
商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
在上述条件不变、商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?(提示:盈利=售价-进价)
.某人2008年初投资120万元于股市,由于无暇操作,第一年的亏损率为20%,以后其亏损率有所变化,至2011年初其股票市值仅为77.76万元,求此人的股票在第二年、第三年平均每年的亏损率.
已知 是关于x的方程。在解这个方程时,粗心的小虎误将
是关于x的方程。在解这个方程时,粗心的小虎误将 看成
看成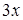 ,得方程解为
,得方程解为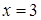 。请你帮助小虎求出原方程的解。
。请你帮助小虎求出原方程的解。
如图,一个用铝合金材料加工的长方形窗框,它的宽和高分别为 厘米,
厘米,
 厘米,解答下列问题(结果可用含
厘米,解答下列问题(结果可用含 ,
, 的代数式表示).
的代数式表示).
(1)长方形窗框的面积是 厘米2;
(2)铝合金窗分为上、下两栏,四周框架和中间隔栏的材料均为宽度6厘米的铝合金
材料,上栏和下栏的框内高度(不含铝合金部分)的比为1:2(接口用料忽略不计).
①求制作一个该种窗框所需铝合金材料的总长度;
②求该种窗框的透光部分的面积.
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)A→C(___,___),B→C(___,___),C→(-3,-4);
(2)若贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)若贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(-2,-1),(+2,+3),(-1,-2),请在图中标出妮妮的位置E点.
(4)在(3)中贝贝若每走1 需消牦1.5焦耳的能量,则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
需消牦1.5焦耳的能量,则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场。一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售。预计每箱水果的盈利情况如下表:
有两种配货方案(整箱配货):
方案一:甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店_________箱,乙店__________箱;B种水果甲店_________箱,乙店__________箱.如果按照方案一配货,请你计算出经销商能盈利多少元?
请你将方案二填写完整(只填写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多?
在甲、乙两店各配货10箱,且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
某地电话拨号上网有两种收费方式,用户可以任 意选择其中一种:第一种是计时制,0.05元/分; 第二种是包月制,69元/月(限一部个人住宅电话上网).此外,每一种上网方式都得加收通讯费0.02元/分.
意选择其中一种:第一种是计时制,0.05元/分; 第二种是包月制,69元/月(限一部个人住宅电话上网).此外,每一种上网方式都得加收通讯费0.02元/分.
(1)若小明家今年三月份上网的时间为 小时,请你分别写出两种收费方式下小明家应该支付的费用;
小时,请你分别写出两种收费方式下小明家应该支付的费用;
(2)若小明估计自家一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示。根据图中的数据(单位:m),解答下列问题:
①用含 、
、 的代数式表示地面总面积;
的代数式表示地面总面积;
②当 ,
, 时,若铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多元?
时,若铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多元?
(本小题共5分)一家三口在假期期间去北方旅游,当地有甲、乙两家旅游社,其定价一样,但对家庭旅游都有优惠,甲旅行社表示大人不打折,小孩打六折;乙旅行社表示一家三口全都打八折,经核算,乙旅行社要便宜240元,问成人定价多少元?
佳 佳和小超玩一个抽卡片游戏:有一叠卡片,每张上面都写着一个数字,二人轮流从中抽取,若抽到的卡片上的数字大于10,
佳和小超玩一个抽卡片游戏:有一叠卡片,每张上面都写着一个数字,二人轮流从中抽取,若抽到的卡片上的数字大于10, 就加上这个数字,若抽到的卡片上的数字不大于10,就减去这个数字.第一轮抽卡完毕(每人抽4张),二人抽到的卡片如下图所示.若规定从0开始计算,结果小者为胜,那么第一轮抽卡谁获胜?
就加上这个数字,若抽到的卡片上的数字不大于10,就减去这个数字.第一轮抽卡完毕(每人抽4张),二人抽到的卡片如下图所示.若规定从0开始计算,结果小者为胜,那么第一轮抽卡谁获胜?
观察下面三行数
1,-2,4,-8,16,-32 …… ①
0,-6,6,-18,30,-66 …… ②
2,-4,8,-16,32,-64 …… ③第③行的数按什么规律排列?
第①、②行的数与第③行的数分别有什么关系?
取每行数的第8个数,计算它们的和。
小王家是新农村建设中涌现出的“养殖专业户”.他准备购置80只相同规格的网箱,养殖A、B两种淡水鱼(两种鱼不能混养).计划用于养鱼的总投资不少于7万元,但不超过7.2万元,其中购置网箱等基础建设需要1.2万元.设他用x只网箱养殖A种淡水鱼,目前平均每只网箱养殖A、B两种淡水鱼所需投入及产业情况如下表:
| 项目类别 |
鱼苗投资 (百元) |
饲料支出 (百元) |
收获成品鱼(千克) |
成品鱼价格 (百元/千克) |
| A种鱼 |
2.3 |
3 |
100 |
0.1 |
| B种鱼 |
4 |
5.5 |
55 |
0.4 |
(1)小王有哪几种养殖方式?
(2)哪种养殖方案获得的利润最大?
(3)根据市场调查分析,当他的鱼上市时,两种鱼的价格会有所变化,A种鱼价格上涨a%(0<a<50),B种鱼价格下降20%,考虑市场变化,哪种方案获得的利润最大?(利润=收入-支出.收入指成品鱼收益,支出包括基础建设投入、鱼苗投资及饲料支出)