如图14,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上,点
的顶点均在格点上,点 的坐标为
的坐标为 .
.
(1)把 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的 ,画出
,画出 ,并写出
,并写出 的坐标;
的坐标;
(2)以原点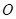 为对称中心,再画出与
为对称中心,再画出与 关于原点
关于原点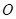 对称的
对称的 ,并写出点
,并写出点 的坐标.
的坐标.
某企业2006年盈利1500万元,2008年克服全球金融危机的不利影响,仍实现盈利2160万元.从2006年到2008年,如果该企业每年盈利的年增长率相同,求:
(1)该企业每年盈利的年增长率多少?
(2)若该企业盈利的年增长率继续保持不变,预计2009年盈利多少万元?
小红爸爸上星期六买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况。(单位:元)
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌 |
+4 |
+4.5 |
-1 |
-2.5 |
-6 |
(1)通过上表你认为星期三收盘时,每股是多少?
(2)本周内每股最高是多少?最低是多少元?
(3)已知小红爸爸买进股票时付了1.5‰的手续费,卖出时还需付成交额,1.5‰的手续费和1‰的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?
已知,如图,在直角梯形COAB中,OC∥AB,以O为原点建立平面直角坐标系,A、B、C三点的坐标分别为A(8,0),B(8,10),C(0,4),
点D为线段BC的中点,动点P从点O出发,以每秒1个单位的速度,沿折线OABD的路线移动,移动的时间为 秒.
秒.
(1)求直线BC的解析式;
(2)若动点P在线段OA上移动,当 为何值时,四边形OPDC的面积是梯形COAB面积的
为何值时,四边形OPDC的面积是梯形COAB面积的 ?
?
(3)动点P从点O出发,沿折线OABD的路线移动过程中,设△OPD的面积为S,请直接写出S与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围。
的取值范围。
阅读下列材料,并解决后面的问题.
材料:一般地,n个相同的因数 相乘:
相乘: 记为
记为 。如23=8,此时,3叫做以2为底8的对数,记为
。如23=8,此时,3叫做以2为底8的对数,记为 。
。
一般地,若 ,则n叫做以
,则n叫做以 为底b的对数,记为
为底b的对数,记为 ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为 。
。
问题:
(1)计算以下各对数的值:
(2)观察(1)中三数4、16、64之间满足怎样的关系式? 之间又满足怎样的关系式?
之间又满足怎样的关系式?
(3)由(2)的结果,你能归纳出一个一般性的结论吗? 
(4)根据幂的运算法则: 以及对数的含义证明上述结论。
以及对数的含义证明上述结论。
证明:
课堂上对关于x的方程: 的解进行合作探究时,甲同学发现,当m=0时,方程的两根都为1,当m>0时,方程有两个不相等的实数根;乙同学发现,无论m取什么正实数时方程的两根都不可能相等;丙同学发现无论m取什么正实数时方程的两根这和均为定值。
的解进行合作探究时,甲同学发现,当m=0时,方程的两根都为1,当m>0时,方程有两个不相等的实数根;乙同学发现,无论m取什么正实数时方程的两根都不可能相等;丙同学发现无论m取什么正实数时方程的两根这和均为定值。
(1)请找一个m的值代入方程使方程的两个根为互不相等的整数,并求这两个根;
(2)请选择乙或丙同学的发现加以判断,并说明理由。
某楼盘准备以每平方米6000元的价格销售,由于国务院有关房地产的新政出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的价格销售。
(1)求平均每次下调的百分率;
(2)某人准备购买一套100平方米的住房,开发商对一次付款有以下两种优惠方案以供选择:①打9.5折销售;②不打折, 一次性送装修费每平方米240元,试问哪种方案更优惠?
阅读下面材料,再回答问题:
有一些几何图形可以被某条直线分成面积相等的两部分,我们将“把一个几何图形分成面积相等的两部分的直线叫做该图形的二分线”,如:圆的直径所在的直线是圆的“二分线”,正方形的对角线所在的直线是正方形的“二分线”。
解决下列问题:
(1)菱形的“二分线”可以是 。
(2)三角形的“二分线”可以是 。
(3)在下图中,试用两种不同的方法分别画出等腰梯形ABCD的“二分线”.
如图,A,B,C是新建的三个居民小区,我们已经在到三个小区距离相等的地方修建了一所学校,现规划修建居民小区D,其要求是:
(1)到学校的距离与其它小区到学校的距离一样;
(2)控制人口密度,有利于生态环境建设,试确定居民小区D的位置.
有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)
如图,有两个边长为2的正方形,将其中一个正方形沿对角线剪开成两个全等的等腰直角三角形,用这三个图片分别在网格备用图的基础上(只要再补出两个等腰直角三角形即可),分别拼出一个三角形、一个四边形、一个五边形、一个六边形.
问题背景 某课外学习小组在一次学习研讨中,得到如下两个命题:
① 如图1,O是正三角形ABC的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 120°,则四边形OPBQ的面积等于三角形ABC面积的三分之一.
② 如图2,O是正方形ABCD的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 90°,则四边形OPBQ的面积等于正方形ABCD面积的四分之一.然后运用类比的思想提出了如下的命题:
③ 如图3,O是正五边形ABCDE的中心,∠MON分别与AB、BC交于点P,Q,若∠MON = 72°,则四边形OPBQ的面积等于五边形ABCDE面积的五分之一.
、任务要求
(1)请你从①、②、③三个命题中选择一个进行证明;(说明:选①做对的得5分,选②做对的得4分,选③做对的得6分)
(2)请你继续完成下面的探索:
如图④,在正n(n≥3)边形ABCDEF…中,O是中心,∠MON分别与AB、BC交于点P,Q,若∠MON等于多少度时,则四边形OPBQ的面积等于正n边形ABCDE…面积的n分之一?(不要求证明)
解:(1)我选 .
证明:
已知抛物线 .
.
(1)该抛物线和 轴的交点坐标是 ▲ ,顶点坐标是 ▲ ;
轴的交点坐标是 ▲ ,顶点坐标是 ▲ ;
(2)选取适当的数据填入下表,并在如图的直角坐标系内描点画出该抛物线的图象;
(3)若该抛物线上两点 的横坐标满足
的横坐标满足 ,试比较
,试比较 与
与 的大小.
的大小.