初中数学应用类问题试题

会堂里竖直挂一条幅AB，如图，小刚从与B成水平的C点观察，视角∠C＝30°，当他沿CB方向前进2米到达到D时，视角∠ADB＝45°，求条幅AB的长度。

问题再现
现实生活中，镶嵌图案在地面、墙面乃至于服装面料设计中随处可见．在八年级课题学习“平面图形的镶嵌”中，对于单种多边形的镶嵌，主要研究了三角形、四边形、正六边形的镶嵌问题．今天我们把正多边形的镶嵌作为研究问题的切入点，提出其中几个问题，共同来探究.

我们知道，可以单独用正三角形、正方形或正六边形镶嵌平面．如右图中，用正方形镶嵌平面，可以发现在一个顶点O周围围绕着4个正方形的内角.
试想：如果用正六边形来镶嵌平面，在一个顶点周围应该围绕着         个
正六边形的内角．
问题提出
如果我们要同时用两种不同的正多边形镶嵌平面，可能设计出几种不同的组合方案？
问题解决
猜想1：是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌？
分析：我们可以将此问题转化为数学问题来解决．从平面图形的镶嵌中可以发现，解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点．具体地说，就是在镶嵌平面时，一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角．
验证1：在镶嵌平面时，设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角．根据题意，可得方程：
，整理得：，
我们可以找到惟一一组适合方程的正整数解为 ．  
结论1：镶嵌平面时，在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌．
猜想2：是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由．
验证2：
结论2：                                                                     
                                                                              
上面，我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况，仅仅得到了一部分组合方案，相信同学们用同样的方法，一定会找到其它可能的组合方案．
问题拓广
请你仿照上面的研究方式，探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案，并写出验证过程．
猜想3：                                                                     .
验证3：
结论3：                                                                     
                                                                                .

如图，点G、D、C在直线a上，点E、F、A、B在直线b上，若从如图所示的位置出发，沿直线b向右匀速运动，直到EG与BC重合．运动过程中与矩形重合部分的面积（S）随时间（t）变化的图象大致是（   ）

如图，填在各方格中的三个数之间均具有相同的规律，根据此规律，n的值是

A．48

B．56

C．63

D．74

某市为治理污水，需要铺设一段全长为的污水排放管道，为了尽量减少施工对城市交通所造成的影响，实际施工时每天的工效比原计划增加，结果提前天完成这一任务，实际每天铺设多长管道？

观察下列图形（每幅图中最小的三角形都是全等的），请写出第个图中最小的三角形的个数有          个．

若与的方向相反，且，，则下列用表示的式子中，正确的是（    ）.

挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走．如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…．则第6次应拿走的是（   ）

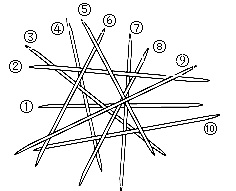
A．②号棒

B．⑦号棒

C．⑧号棒

D．⑩号棒

妈妈让小明给客人烧水沏茶，洗开水壶要用1分钟，烧开水要用15分钟，洗茶壶要用1分钟，洗茶杯要用1分钟，放茶叶要用2分钟，给同学打电话要用1分钟．为使客人早点喝上茶，小明最快可在几分钟内完成这些工作？

A．19分钟

B．18分钟

C．17分钟

D．16分钟

用边长相等的三角形、四边形、五边形、六边形、七边形中的一种；能进行平面镶嵌的几何图形有         种．

小明用两根同样长的竹棒做对角线，制作四边形的风筝，则该风筝的形状一定是（ 　）

A．矩形

B．正方形

C．等腰梯形

D．无法确定

某校七年级学生到野外活动，为测量一池塘两端A，B的距离，甲、乙、丙三位同学分别设计出如下几种方案：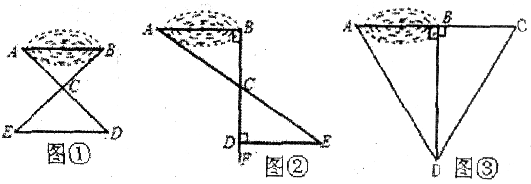

甲：如图①，先在平地取一个可直接到达A，B的点C，再连接AC，BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的长即为A，B的距离。
乙：如图②，先过点B作AB的垂线BF，再在BF上取C，D两点，使BC=CD，接着过点D作BD的垂线DE，交AC的延长线于点E，则测出DE的长即为A，B的距离。
丙：如图③，过点B作BD⊥AB，再由点D观测，在AB的延长线上取一点C，使∠BDC=∠BDA，这时只要测出BC的长即为A，B的距离。
（1）以上三位同学所设计的方案，可行的有_______________；
（2）请你选择一可行的方案，说说它可行的理由。

如图，一艘科学考察船由港口A出发沿正北方向航行，在航线的一侧有两个小岛C、D．考察船在A处时，测得小岛C在船的正西方，小岛D在船的北偏西30°方向．考察船向北航行了12千米到B处时，测得小岛C在船的南偏西30°方向，小岛D在船的南偏西60°方向．求小岛C、D之间的距离．

晚上，小亮走在大街上．他发现：当他站在大街两边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3米，左边的影子长为1.5米．又知自己身高1.80米，两盏路灯的高相同，两盏路灯之间的距离为12米，则路灯的高为　　　　米．

按下面的要求填空，完成本题的解答．
青山村种的水稻2007年平均每公顷产8 000 kg，2009年平均每公顷产9 680 kg，
求该村水稻每公顷产量的年平均增长率.
解：设该村水稻每公顷产量的年平均增长率为.
（Ⅰ）用含的代数式表示：
① 2008年种的水稻平均每公顷的产量为                      kg；
② 2009年种的水稻平均每公顷的产量为                      kg；
（Ⅱ）根据题意，列出相应方程                             ；
（Ⅲ）解这个方程，得                             ；
（Ⅳ）检验：                                                           ；
（Ⅴ）答：该村水稻每公顷产量的年平均增长率为                         %.