[江西]2012-2013学年江西省吉安市七校七年级下学期联考数学试卷
下列事件为必然事件的是( )
| A.小平本次数学考试中,成绩将是105分 |
| B.某射击运动员射靶一次,正中靶心 |
| C.打开电视机,CCTV第一套节目正在播放新闻 |
| D.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
如图,下列条件中,能判定DE//AC的是( )
| A.∠BED=∠EFC | B.∠1=∠2 | C.∠3=∠4 | D.∠BEF+∠B=180° |
如图,三角形纸片ABC,AB=12cm,BC=7cm,AC=8cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
| A.8 cm | B.9 cm | C.11 cm | D.13 cm |
如图,△ABC中BC边上的高为h1,AB边上的高为h2,△DEF中DE边上的高为h3,下列结论正确的是( )
| A.h1=h2 | B.h2=h3 | C.h1=h3 | D.无法确定 |
如图,已知AB平分∠CBD,请你补充一个条件:___________,使得△ABD≌△ABC。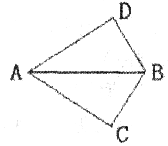
H7N9是一种新型禽流感,于2013年3月底在上海和安徽两地率先发现。禽流感病毒球形直径约125纳米,1纳米=0.000000001米,请用科学记数法表示125纳米=_________米。
如图,直线a//b,将含有45°角的三角形板ABC的直角顶点C放在直线b上,若∠1=27°,则∠2的度数为______________。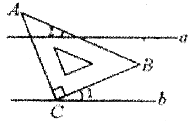
若等腰三角形两条边的长分别是11cm和23cm,则该三角形的周长是____________。
下面共有四种情景:
A. 一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系);
B. 从树上开始往下掉的苹果(苹果落地前的高度与下落时间的关系);
C. 一杯越来越凉的开水(水温与时间的关系);
D. 竖直向上抛出的篮球(篮球落地前的速度与时间的关系);
上面各种情景可以近似的用下面那个图象来表示(横轴表示时间,纵轴表示相应的因变量),A、B、C、D各情景对应的图象依次为:___________。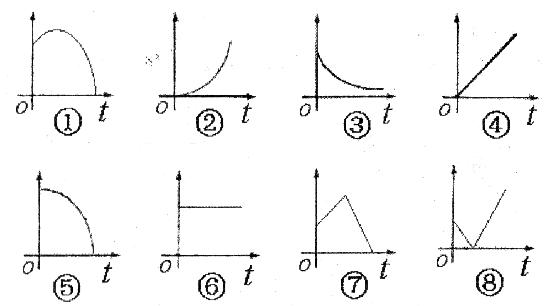
如图,已知等腰三角形△ABC,其中AB=AC,∠CAB=40°,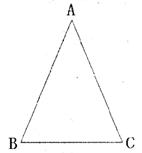
(1)作底角∠ABC的平分线BD,交AC于点D(要求用尺规作图,不用写作法,但要保留作图痕迹)
(2)请计算∠BDC的度数。
如图,在3×3的正方形网格图中,格点△ABC和△DEF关于某直线成轴对称,请你在下面备用图中分别画出一个符合条件的△DEF。
一颗木质的中国象棋子“帅”,它的正面雕刻一个“帅”字,它的反面是平的,将它从一定高度掷下,落地反弹后可能是“帅”字面朝上,也可能是“帅”字面朝下,由于棋子的两面不均匀,为了估计“帅”字面朝上的概率,七年级某实验小组做了掷棋子的试验,试验数据如下表:
| 试验次数 |
20 |
80 |
100 |
160 |
200 |
240 |
300 |
360 |
400 |
| “帅”字朝上的频数 |
14 |
48 |
50 |
84 |
112 |
144 |
172 |
204 |
228 |
| 相应的频率 |
0.70 |
0.60 |
0.50 |
0.53 |
|
0.60 |
|
0.57 |
|
(1)请将上数据表补充完整;
(2)根据上表,画出“帅”字面朝上的频率的折线统计图;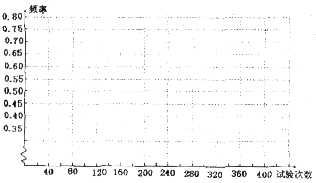
(3)如将试验继续进行下去,根据上表的数据,这个试验的频率将稳定在它的概率附近,请你估计这个概率是多少?
某校七年级学生到野外活动,为测量一池塘两端A,B的距离,甲、乙、丙三位同学分别设计出如下几种方案: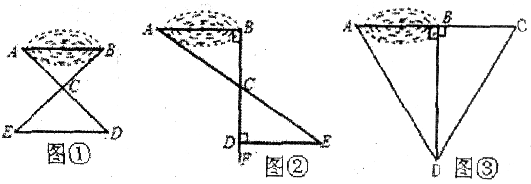
甲:如图①,先在平地取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的长即为A,B的距离。
乙:如图②,先过点B作AB的垂线BF,再在BF上取C,D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出DE的长即为A,B的距离。
丙:如图③,过点B作BD⊥AB,再由点D观测,在AB的延长线上取一点C,使∠BDC=∠BDA,这时只要测出BC的长即为A,B的距离。
(1)以上三位同学所设计的方案,可行的有_______________;
(2)请你选择一可行的方案,说说它可行的理由。
弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的重量(kg)之间的关系如下表:
| 所挂物体的重量(kg) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 弹簧的长度(cm) |
12 |
12.5 |
13 |
13.5 |
14 |
14.5 |
15 |
15.5 |
(1)当所挂物体的重量为3kg时,弹簧的长度是_____________cm;
(2)如果所挂物体的重量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(3)当所挂物体的重量为5.5kg时,请求出弹簧的长度。
(4)如果弹簧的最大伸长长度为20cm,则该弹簧最多能挂多重的物体?
如图,在四边形ABCD中,∠A=104°,∠ABC=76°,BD⊥CD于点D,EF⊥CD于点F,你能说明∠1=∠2吗?试一试。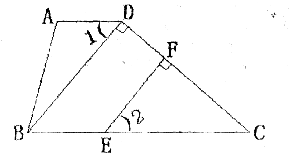
乘法公式的探究及应用:
探究问题:
如图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2,如图所示。
(1)则图1长方形纸条的面积可表示为________________(写成多项式乘法的形式)。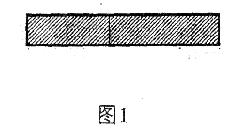
(2)拼成的图2中阴影部分面积可表示为________________(写成两数平方差的形式)。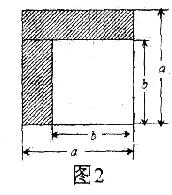
(3)比较两图的阴影部分面积,可以得到乘法公式____________。
结论运用:
(4)应用所得的公式计算: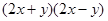 =____________________。
=____________________。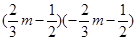 =___________________。
=___________________。
拓展运用:
(5)计算: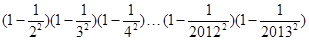 。
。





 是一个完全平方式,则m=_______________。
是一个完全平方式,则m=_______________。 ,
, ,则
,则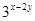 的值为_____________。
的值为_____________。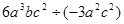 。
。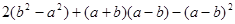 ,其中
,其中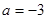 ,b=2。
,b=2。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号