如图1，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E。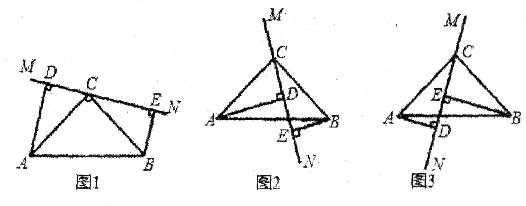
（1）①写出图1中的一对全等三角形；②写出图1中线段DE、AD、BE所具有的等量关系；（不必说明理由）
（2）当直线MN绕点C旋转到图2的位置时，请说明DE=AD－BE的理由；
（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系（不必说明理由）。
相关试题
的值，其中
.
，B
，且多项式
的值与字母
的取值无关，求
的值.
如图，直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边△AOB，点C为
正半轴上一动点（OC＞1），连结BC，以线段BC为边在第四象限内作等边△CBD，直线DA交
轴于点E．
（1）△OBC与△ABD全等吗？判断并证明你的结论；
（2）将等边△AOB沿轴翻折，B点的对称点为B'
①点B'会落在直线DE上么？请说明理由．
②随着点C位置的变化，点E的位置是否会发生变化? 若没有变化，求直接写出点E
相关知识点
推荐套卷
粤公网安备 44130202000953号