对x,y定义一种新运算T,规定:T(x,y)= (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= =b.
=b.
(1)已知T(1,-1)=-2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
上海某宾馆客房部有三人普通间和二人普通间,每间收费标准如下表所示.世博会期间,一个由50名女工组成的旅游团人住该宾馆,她们都选择了三人普通间和二人普通间,且每间正好都住满.设该旅游团人住三人普通间有x间.
(1)该旅游团人住的二人普通间有________间(用含x的代数式表示);
(2)该旅游团要求一天的住宿费必须少于4500元,且入住的三人普通间不多于二人普通间.若客房部能满
足该旅游团的要求,那么该客房部有哪几种安排方案?
| 客房 |
普通间(元/天) |
| 三人间 |
240 |
| 二人间 |
200 |
一次函数y=k x+b的图像经过点(0,-4)且与正比例函数y=k
x+b的图像经过点(0,-4)且与正比例函数y=k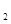 x的图象交于点(2,-1).
x的图象交于点(2,-1).
(1)分别求出这两个函数的表达式;
(2)求这两个函数的图象与x轴围成的三角形的面积;
(3)直接写出不等式k x-4≥k
x-4≥k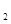 x的解集。
x的解集。
某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润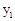 (元)与国内销售数量
(元)与国内销售数量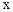 (千件)的关系为:
(千件)的关系为: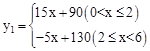 若在国外销售,平均每件产品的利润
若在国外销售,平均每件产品的利润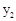 (元)与国外的销售数量t(千件)的关系为:
(元)与国外的销售数量t(千件)的关系为:
(1)用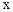 的代数式表示t为:t=;当0<
的代数式表示t为:t=;当0<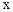 ≤4时,
≤4时,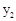 与
与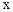 的函数关系式为:
的函数关系式为: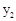 =;当4≤
=;当4≤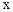 <时,
<时, =100;
=100;
(2)求每年该公司销售这种健身产品的总利润W(千元)与国内的销售数量x(千件)的函数关系式,并指出x的取值范围;
(3)该公司每年国内、国外的销量各为多少时,可使公司每年的总利润最大?最大值为多少?
为支援四川雅安地震灾区,某市民政局组织募捐了240吨救灾物资,现准备租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载货量和租金如下表:
| 甲种货车 |
乙种货车 |
|
| 载货量(吨/辆) |
45 |
30 |
| 租金(元/辆) |
400 |
300 |
如果计划租用6辆货车,且租车的总费用不超过2300元,求最省钱的租车方案.
郑州市花卉种植专业户王有才承包了30亩花圃,分别种植康乃馨和玫瑰花,有关成本、销售额见下表:
| 种植种类 |
成本(万元/亩) |
销售额(万元/亩) |
| 康乃馨 |
2.4 |
3 |
| 玫瑰花 |
2 |
2.5 |
(1)2012年,王有才种植康乃馨20亩、玫瑰花10亩,求王有才这一年共收益多少万元?(收益=销售额-成本)
(2)2013年,王有才继续用这30亩花圃全部种植康乃馨和玫瑰花,计划投入成本不超过70万元.若每亩种植的成本、销售额与2012年相同,要获得最大收益,他应种植康乃馨和玫瑰花各多少亩?
(3)已知康乃馨每亩需要化肥500kg,玫瑰花每亩需要化肥700kg,根据(2)中的种植亩数,为了节约运输成本,实际使用的运输车辆每次装载化肥的总量是原计划每次装载总量的2倍,结果运输全部化肥比原计划减少2次.求王有才原定的运输车辆每次可装载化肥多少千克?
苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:
①每亩水面的年租金为500元,水面需按整数亩出租;
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1400元收益;
④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
(1)若租用水面n亩,则年租金共需元;
(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润:收益—成本);
(3)李大爷现有资金25000元,他准备再向银行贷不超过25000元的款。用于蟹虾混合养殖。已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元.可使年利润超过35000元?
某公司拟为贫困山区建一所希望小学,甲、乙两个工程队提交了投标方案,若独立完成该项目,则甲工程队所用时间是乙工程队的1.5倍;若甲、乙两队合作完成该项目,则共需72天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)若由甲工程队单独施工,平均每天的费用为0.8万元,为了缩短工期,该公司选择了乙工程队,但要求其施工的总费用不能超过甲工程队,求乙工程队平均每天的施工费用最多为多少万元?
﹣(本题12分)在一平直河岸 同侧有
同侧有 两个村庄,
两个村庄, 到
到 的距离分别是3km和2km,
的距离分别是3km和2km,
 .现计划在河岸
.现计划在河岸 上建一抽水站
上建一抽水站 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图(1)是方案一的示意图,设该方案中管道长度为 ,且
,且 (其中
(其中 于点
于点 );图(2)是方案二的示意图,设该方案中管道长度为
);图(2)是方案二的示意图,设该方案中管道长度为 ,且
,且 (其中点
(其中点 与点
与点 关于
关于 对称,
对称, 与
与 交于点
交于点 ).
).
 |
(1)观察计算
在方案一中, km(用含
km(用含 的式子表示);
的式子表示);
在方案二中,组长小宇为了计算 的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算, km(用含
km(用含 的式子表示).
的式子表示).
(2)探索归纳
①当 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
当 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”); ②请你参考右边方框中的方法指导,
②请你参考右边方框中的方法指导,
就 (当
(当 时)的所有取值情况进
时)的所有取值情况进
行分析,要使铺设的管道长度较短,
应选择方案一还是方案二?
(本小题满分9分)
已知关于 的方程
的方程 有两个不相等的实数根
有两个不相等的实数根 、
、 ,问是否存在实数
,问是否存在实数 ,使方程的两实数根互为相反数?如果存在,求出
,使方程的两实数根互为相反数?如果存在,求出 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
如图,用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉未进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的 ,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a cm,若铁钉总长度为6cm,则a的取值范围是.
,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a cm,若铁钉总长度为6cm,则a的取值范围是.
不等式组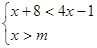 的解集是
的解集是 >3,则m的取值范围是
>3,则m的取值范围是
| A.m=3 | B.m≥3 | C.m≤3 | D.m<3 |
小明参加学校组织的知识竞赛,共有 道题.答对一题记
道题.答对一题记 分,答错(或不答)一题记
分,答错(或不答)一题记 分,小明参加本次竞赛要超过
分,小明参加本次竞赛要超过 分,他至少要答对多少道题?
分,他至少要答对多少道题?