如图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长为1,则这个六边形的周长是 (17届江苏初一1试)如图 如 .
某公司生产一种饮料是由A,B两种原料液按一定比例配制而成,其中A原料液的成本价为15元/千克,B原料液的成本价为10元/千克,按现行价格销售每千克获得70%的利润率.由于市场竞争,物价上涨,A原料液上涨20%,B原料液上涨10%,配制后的总成本增加了12%,公司为了拓展市场,打算再投入现总成本的25%做广告宣传,如果要保证每千克利润不变,则此时这种饮料的利润率是
若将一个两位数的十位数字与个位数字对调后所得的新两位数是其数字和的3倍,则原两位数是 ;
先阅读短文,然后回答短文后面所给出的问题:
对于三个数a、b、c的平均数,最小的数都可以给出符号来表示,我们规定 表示这三个数的平均数,
表示这三个数的平均数,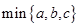 表示这三个数中的最小的数,
表示这三个数中的最小的数, 表示这三个数中最大的数.例如:
表示这三个数中最大的数.例如: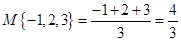 ,
,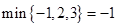 ,
,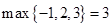 ;
; ,
, .
.
(1)请填空: ;若
;若 ,则
,则 ;
;
(2)若 ,求
,求 的取值范围;
的取值范围;
(3)若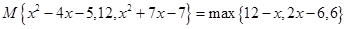 ,求
,求 的值.
的值.
甲、乙、丙三个教师承担本学期期末考试的第17题的网上阅卷任务,若由这三人中的某一人独立完成阅卷任务,则甲需要15小时,乙需要10小时,丙需要8小时。
(1)如果甲、乙、丙三人同时改卷,那么需要多少时间完成?
(2)如果按照甲、乙、丙、甲、乙、丙、……的次序轮流阅卷,每一轮中每人各阅卷1小时。那么要多少小时完成?
(3)能否把(2)题所说的甲、乙、丙的次序作适当调整,其余的不变,使得完成这项任务的时间至少提前半小时?(答题要求:如认为不能,需要说明理由;如认为能,请至少说出一种轮流的次序,并求出相应能提前多少时间完成阅卷任务)
甲杯中盛有红墨水若干ml,乙杯中盛有蓝墨水若干ml,现在用一个容积为50ml
的小杯子从甲杯中盛走一小杯红墨水倾入乙杯,待乙杯中两种墨水混合均匀后;从乙杯中盛
走一小杯混合液倾入甲杯中,试问,这时乙杯中的红墨水的液量和甲杯中混进来的蓝墨水的
液量相比,哪个多?
| A.甲杯蓝墨水多,乙杯红墨水少 | B.甲杯蓝墨水少,乙杯红墨水多 |
| C.甲杯蓝墨水与乙杯红墨水一样多甲 | D.无法判定 |
(本题10分)同学们都知道: 表示
表示 与
与 之差的绝对值,实际上也可理解为
之差的绝对值,实际上也可理解为 与
与 两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:

(1) 数轴上表示 与
与 两点之间的距离是________,
两点之间的距离是________,
(2) 数轴上表示 与
与 的两点之间的距离可以表示为__ ________.
的两点之间的距离可以表示为__ ________.
(3) 如果 ,则
,则 = .
= .
(4) 同理 表示数轴上有理数x所对应的点到-3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得
表示数轴上有理数x所对应的点到-3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得 =4,这样的整数是 .
=4,这样的整数是 .
(5) 由以上探索猜想对于任何有理数 ,
, 是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
某单位购买35张电影票共用250元,其中甲种票每张8元,乙种票每张6元,则购买甲、乙两种票的数量分别为 .
今年3.15期间,惠东商场为感谢新老顾客,决定对某产品实行优惠政策:购买该产品,另外赠送礼品一份. 经过与该产品的供应商协调,供应商同意将该产品供货价格降低5%,同时免费为顾客提供礼品;而该产品的商场零售价保持不变. 这样一来,该产品的单位利润率由原来的x%提高到(x+6)%,则x的值是_______________________.
阅读下列材料:
为落实开展社会大课堂活动,七年级(3)班李老师准备周六组织本班学生参观北京科技馆,要求学生周六早9:00准时在科技馆门前集合,然后几种买票参观.
小强家离北京科技馆4公里,周六他准备乘出租车去,为了解北京出租车的计价方式,小强周五晚上在网上查到了现行北京市出租车价格标准:
| 收费项目 |
收费标准 |
| 3公里以内收费 |
13元 |
| 基本单价 |
2.3元/公里 |
| 低速行驶和等候费 |
根据乘客要求停车等候或由于道路条件限制,时速低于12公里时,每5分钟早晚高峰期间加收2公里租价(不含空驶费)其他时间段加收1公里租价(不含空驶费) |
| 预约叫车服务费 |
提前4小时以上预约每次6元,4小时以内预约每次5元 |
| 空驶费 |
单程旅客行驶超过15公里部分,基本单价加收50%的费用,往返载客(即起点和终点在2公里(含)范围以内)不加收空驶费 |
| 夜间收费 |
23:00(含)至次日5:00(不含)运营时,基本单价加收20%的费用 |
| 合乘收费 |
合乘里程部分,按非合乘情况下应付金额的60%付费 |
| 燃油附加费 |
1元/运次 |
| 备注:1、早高峰7:00(含)﹣﹣9:00(不含);晚高峰17:00(含)﹣﹣19:00(不含). 2、出租车计价段里程精确到500米,时间精确到2.5分钟;出租汽车收费结算以元为单位,元以下四舍五入. 3、过路、过桥费由乘客负担. 4、按日结算的包车及出北京行政区域的客运业务收费实行市场调节价. |
在仔细阅读标准后,小强准备周六早上8点10分乘车,路上留出10分钟出租车时速低于12公里的堵车时间,这样在9点之前一定能顺利到达科技馆.时间设计好后,经过计算小强向妈妈要30元打车钱,妈妈问他30元钱够吗?小强说:“我按上表计算了,30元钱还有几块钱的剩余呢.”
下面是小强的分析与计算过程,请补充完整:
(1)小强在计算所需出租车费用时,用到上表中的信息包括 .
(2)路上堵车10分钟,小强计算这10分钟出租车的低速行驶费用是多少?
(3)小强说:“我按上表计算了,30元钱还有几块钱的剩余呢.”请你计算小强的打车费用和剩余钱数.
如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米,
(1)若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;
(2)观察图形的特点可知,长方形相对的两边是相等的(如图中的MN和PQ).请根据这个等量关系,求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?
(本题10分)用正方形硬纸板做三棱柱盒子,每个盒子由 个矩形侧面和
个矩形侧面和 个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)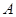 方法:剪
方法:剪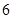 个侧面;
个侧面;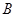 方法:剪
方法:剪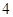 个侧面和
个侧面和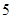 个底面.
个底面.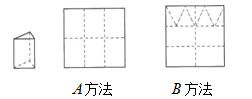
现有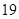 张硬纸板,裁剪时
张硬纸板,裁剪时 张用
张用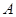 方法,其余用
方法,其余用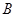 方法.
方法.
(1)用 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
如图:在数轴上A点表示数 ,B点示数
,B点示数 ,C点表示数c,b是最小的正整数,
,C点表示数c,b是最小的正整数,
且a、b满足|a+2|+ (c-7)2=0.
(1)a= ,b= ,c= ;
(2)若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.
则AB= ,AC= ,BC= .(用含t的代数式表示)
(4)请问:3BC-2AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
上海某宾馆客房部有三人普通间和二人普通间,每间收费标准如下表所示.世博会期间,一个由50名女工组成的旅游团人住该宾馆,她们都选择了三人普通间和二人普通间,且每间正好都住满.设该旅游团人住三人普通间有x间.
(1)该旅游团人住的二人普通间有________间(用含x的代数式表示);
(2)该旅游团要求一天的住宿费必须少于4500元,且入住的三人普通间不多于二人普通间.若客房部能满
足该旅游团的要求,那么该客房部有哪几种安排方案?
| 客房 |
普通间(元/天) |
| 三人间 |
240 |
| 二人间 |
200 |