初中数学有理数无理数的概念与运算解答题

已知x和y是实数，举例说明下列说法是错误的．
（1）│x+y│=│x│+│y│；（2）若x≤y，则x²≤y²．

如图是一个“数值转换机”（箭头是指数进入转换机的路径,方框是对进入的数进行转换的转换机）。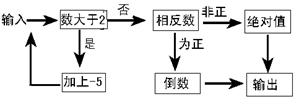

（1）、当小明输入4, 7, -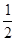 ,-2012 这四个数使,则四次输出的结果依次为       ,       ,       ,       。
（2）、你认为当输入数 等于            时（写出一个即可）,其输出结果为0。
（3）、你认为这个“数值转换机”不可能输出       数。
（4）、有一次,小明在操作的时候,输出的结果是2,聪明的你判断一下,小明输入的正整数是
          （用含自然数n的代数式表示）。

已知: ,……
(1)按照上面算式,你能猜出=                  ;
(2)利用上面的规律计算: 的值.

计算： ．

计算：

计算：

如图，一个点从数轴上的原点开始，先向右移动3个单位长度，再向左移动5个单位长度，可以看到终点表示的数是－2。

已知点A是数轴上的点，完成下列各题：
如果点A表示的数是3，将点A先向左移动7个单位长度，再向右移动5个单位长度，那么终点B表示的数是__________，A、B两点间的距离为__________；
如果点A表示的数是－4，将点A先向右移动168个单位长度，再向左移动256个单位长度，那么终点B表示的数是__________，A、B两点间的距离为__________；
一般地，如果点A表示的数是m，将点A先向右移动n个单位长度，再向左移动t个单位长度，那么终点B表示的数是__________，A、B两点间的距离为__________。

小颖家去年的饮食支出3600元，教育支出1200元，其他支出7200元，小颖家今年的这三项支出依次比去年增长了9%，30%，6%，请你帮小颖算一算今年的总支出比去年增长的百分数是多少？
小明这样帮她算的：(9%＋30%＋6%)=15%
你认为他这样计算对吗？为什么？

阅读下列材料，并解决后面的问题．
材料：一般地，n个相同的因数相乘，记为aⁿ．如2³＝8，此时，3叫做以2为底8的对数，记为log₂8（即log₂8＝3）．一般地，若aⁿ＝b（a＞0且a≠1，b＞0），则n叫做以a为底的对数，记为log_ab（即log_ab＝n）．若3⁴＝81，则4叫做以3为底81的对数，记为log₃81（即log₃81＝4）．问题：
（1）计算以下各对数的值：log₂4＝________，log₂16＝________，log₂64＝________；
（2）观察（1）中三数4，16，64之间满足怎样的关系式？log₂4，log₂16，log₂64之间又满足怎样的关系式？
（3）由（2）的结果，你能归纳出一个一般性的结论吗？log_aM＋log_aN＝________（a＞0且a≠1，M＞0，N＞0）；
（4）根据幂的运算法则：aⁿ·a^m＝a^n＋m以及对数的含义证明上述结论。

观察图形，解答问题：

（1）按下表已填写的形式填写表中的空格：

	图①	图②	图③
三个角上三个数的积	1×（-1）×2=-2	（-3）×（-4）×（-5）=-60
三个角上三个数的和	1+（-1）+2=2	（-3）+（-4）+（-5）=-12
积与和的商	-2÷2=-1，

请用你发现的规律求出图④中的数y和图⑤中的数x．

某车床生产一种工件，该工件的标准直径为，下面是从中抽取的5个工件的检测结果(单位:)：305，408，402，380，405.该车床所生产的工件的合格率是多少?

已知下列各数：-5，，4，0，-1.5，5，，-.把上述各数填在相应的集合里：
正有理数集合：｛                    ｝    负有理数集合：｛                  ｝
分数集合：  ｛                  ｝

探索规律:将连续的偶数2，4，6，8， ，排成下表，如图：

(1)十字框中的五个数的和与中间的数18有什么关系？
(2)设中间的数为x ，用代数式表示十字框中的五个数的和；
(3)若将十字框上下左右移动，可框住另外的五位数，其它五位数的和能等于2050吗？如能，写出这五位数，如不能，说明理由.

如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．

（1）写出数轴上点B表示的数         ，点P表示的数       （用含t的代数式表示）；
（2）动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？
（3）若M为AP的中点，N为PB的中点．点P在运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由；若不变，请你画出图形，并求出线段MN的长；
（4）若点D是数轴上一点，点D表示的数是x，请你探索式子是否有最小值？如果有，直接写出最小值；如果没有，说明理由．

按如图所示的程序计算，若开始输入的x的值为48，我发现第一次得到的结果为24，第二次得到的结果为12，…，请你探索：

（1）第四次得到的结果；（2）第九次得到的结果；（3）第2012次得到的结果．