初中数学列表法与树状图法试题

为庆祝中国共产党成立100周年，在中小学生心中厚植爱党情怀，我市开展“童心向党”教育实践活动，某校准备组织学生参加唱歌，舞蹈，书法，国学诵读活动,为了解学生的参与情况，该校随机抽取了部分学生进行“你愿意参加哪一项活动”（必选且只选一种）的问卷调查．根据调查结果绘制了条形统计图和扇形统计图，部分信息如下：

（1）这次抽样调查的总人数为 　　人，扇形统计图中“舞蹈”对应的圆心角度数为 　　；

（2）若该校有1400名学生，估计选择参加书法的有多少人？

（3）学校准备从推荐的4位同学（两男两女）中选取2人主持活动，根据画树状图或表格法求恰为一男一女的概率．

我们对一个三角形的顶点和边都赋给一个特征值，并定义：从任意顶点出发，沿顺时针或逆时针方向依次将顶点和边的特征值相乘，再把三个乘积相加，所得之和称为此三角形的顺序旋转和或逆序旋转和．如图1， $\mathit{ar}+\mathit{cq}+\mathit{bp}$ 是该三角形的顺序旋转和， $\mathit{ap}+\mathit{bq}+\mathit{cr}$ 是该三角形的逆序旋转和．已知某三角形的特征值如图2，若从1，2，3中任取一个数作为 $x$ ，从1，2，3，4中任取一个数作为 $y$ ，则对任意正整数 $z$ ，此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是 　　．

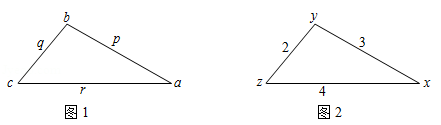
从一副普通的扑克牌中取出四张牌，它们的牌面数字分别为2，3，3，6．

（1）将这四张扑克牌背面朝上，洗匀，从中随机抽取一张，则抽取的这张牌的牌面数字是3的概率为 　　；

（2）将这四张扑克牌背面朝上，洗匀．从中随机抽取一张，不放回，再从剩余的三张牌中随机抽取一张．请根据画树状图或列表的方法，求抽取的这两张牌的牌面数字恰好相同的概率．

近日，教育部印发了《关于举办第三届中华经典诵写讲大赛的通知》，本届大赛以“传承中华经典，庆祝建党百年”为主题，分为“诵读中国”经典诵读，“诗教中国”诗词讲解，“笔墨中国”汉字书写，“印记中国”印章篆刻比赛四类（依次记为 $A$， $B$， $C$， $D)$．为了解同学们参与这四类比赛的意向，某校学生会从有意向参与比赛的学生中随机抽取若干名学生进行了问卷调查（调查问卷如图所示），所有问卷全部收回，并将调查结果绘制成统计图和统计表（均不完整）．

“中华经典诵写讲大赛”参赛意向调查问卷 请在下列选项中选择您有参赛意向的选项，在其后“ $[??]$”内打“ $\surd$”，非常感谢您的合作． $A$．“诵读中国”经典诵读 $[??]$ $B$．“诗教中国”诗词讲解 $[??]$ $C$．“笔墨中国”汉字书写 $[??]$ $D$．“印记中国”印章篆刻 $[??]$

请根据图表提供的信息，解答下列问题：

（1）参与本次问卷调查的总人数为 　　人，统计表中 $C$的百分比 $m$为 　　；

（2）请补全统计图；

（3）小华想用扇形统计图反映有意向参与各类比赛的人数占被调查总人数的百分比，是否可行？若可行，求出表示 $C$类比赛的扇形圆心角的度数；若不可行，请说明理由．

（4）学校“诗教中国”诗词讲解大赛初赛的规则是：组委会提供“春”“夏”“秋”“冬”四组题目（依次记为 $C$， $X$， $Q$， $D)$，由电脑随机给每位参赛选手派发一组，选手根据题目要求进行诗词讲解，请用列表或画树状图的方法求甲，乙两名选手抽到的题目在同一组的概率．

某中学为组织学生参加庆祝中国共产党成立100周年书画展评活动，全校征集学生书画作品．王老师从全校20个班中随机抽取了 $A$ ， $B$ ， $C$ ， $D$ 四个班，对征集作品进行了数量分析统计，绘制了如下两幅不完整的统计图．

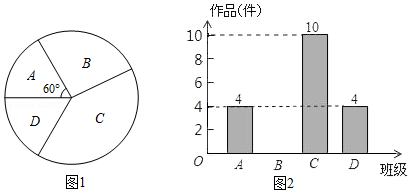
（1）王老师采取的调查方式是 　　（填"普查"或"抽样调查" $)$ ，王老师所调查的4个班共征集到作品 　　件，并补全条形统计图；

（2）在扇形统计图中，表示 $C$ 班的扇形圆心角的度数为 　　；

（3）如果全校参展作品中有4件获得一等奖，其中有1件作品的作者是男生，3件作品的作者是女生．现要从获得一等奖的作者中随机抽取两人去参加学校的总结表彰座谈会，求恰好抽中一男一女的概率．（要求用树状图或列表法写出分析过程）

2021年是中国共产党成立100周年．为普及党史知识，培养爱国主义精神，今年五月份，某市党校举行党史知识竞赛，每个班级各选派15名学员参加了网上测试，现对甲、乙两班学员的分数进行整理分析如下：

甲班15名学员测试成绩（满分100分）统计如下：

87，84，88，76，93，87，73，98，86，87，79，85，84，85，98．

乙班15名学员测试成绩（满分100分）统计如下：

77，88，92，85，76，90，76，91，88，81，85，88，98，86，89

（1）按如表分数段整理两班测试成绩

班级	$70.5~75.5$	$75.5~80.5$	$80.5~85.5$	$85.5~90.5$	$90.5~95.5$	$95.5~100.5$
甲	1	2	$a$	5	1	2
乙	0	3	3	6	2	1

表中 $a=$　　；

（2）补全甲班15名学员测试成绩的频数分布直方图；

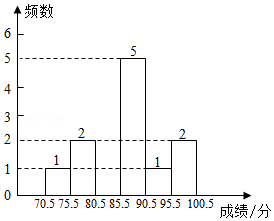
（3）两班测试成绩的平均数、众数、中位数、方差如表所示：

班级	平均数	众数	中位数	方差
甲	86	$x$	86	44.8
乙	86	88	$y$	36.7

表中 $x=$　　， $y=$　　．

（4）以上两个班级学员掌握党史相关知识的整体水平较好的是 　　班；

（5）本次测试两班的最高分都是98分，其中甲班2人，乙班1人．现从以上三人中随机抽取两人代表党校参加全市党史知识竞赛，根据树状图或表格求出恰好抽取甲、乙两班各一人参加全市党史知识竞赛的概率．

在一个不透明的袋子里装有5个小球，每个球上都写有一个数字，分别是1，2，3，4，5，这些小球除数字不同外其它均相同．从中随机一次摸出两个小球，小球上的数字都是奇数的概率为 $($ 　　 $)$

A．

$\frac{6}{25}$

B．

$\frac{9}{25}$

C．

$\frac{3}{10}$

D．

$\frac{3}{5}$

为庆祝中国共产党成立100周年，落实教育部《关于在中小学组织开展“从小学党史，永远跟党走”主题教育活动的通知》要求，某学校举行党史知识竞赛，随机调查了部分学生的竞赛成绩，绘制成两幅不完整的统计图表．根据统计图表提供的信息，解答下列问题：

（1）本次共调查了 　　名学生； $C$组所在扇形的圆心角为 　　度；

（2）该校共有学生1600人，若90分以上为优秀，估计该校优秀学生人数为多少？

（3）若 $E$组14名学生中有4人满分，设这4名学生为 $E1$， $E2$， $E3$， $E4$，从其中抽取2名学生代表学校参加上一级比赛，请用列表或画树状图的方法求恰好抽到 $E1$， $E2$的概率．

竞赛成绩统计表（成绩满分100分）

组别	分数	人数
$A$组	$75<x⩽80$	4
$B$组	$80<x⩽85$
$C$组	$85<x⩽90$	10
$D$组	$90<x⩽95$
$E$组	$95<x⩽100$	14
合计

现有4盒同一品牌的牛奶，其中2盒已过期，随机抽取2盒，至少有一盒过期的概率是 $($ 　　 $)$

A．

$\frac{1}{2}$

B．

$\frac{2}{3}$

C．

$\frac{3}{4}$

D．

$\frac{5}{6}$

有四张大小和背面完全相同的不透明卡片，正面分别印有等边三角形、平行四边形、菱形和圆，将这四张卡片背面朝上洗匀，从中随机抽取两张卡片，所抽取的卡片正面上的图形都既是轴对称图形，又是中心对称图形的概率是 　　．

某校为了解九年级学生体质健康情况，随机抽取了部分学生进行体能测试，并根据测试结果绘制了不完整的条形统计图和扇形统计图，请回答下列问题．

（1）在这次调查中，"优秀"所在扇形的圆心角的度数是 　　；

（2）请补全条形统计图；

（3）若该校九年级共有学生1200人，则估计该校"良好"的人数是 　　；

（4）已知"不及格"的3名学生中有2名男生、1名女生，如果从中随机抽取两名同学进行体能加试，请用列表法或画树状图的方法，求抽到两名男生的概率是多少？

2021年5月，菏泽市某中学对初二学生进行了国家义务教育质量检测，随机抽取了部分参加15米折返跑学生的成绩，学生成绩划分为优秀、良好、合格与不合格四个等级，学校绘制了如下不完整的统计图．根据图中提供的信息解答下列问题：

（1）请把条形统计图补充完整；

（2）合格等级所占百分比为 　　 $\%$ ；不合格等级所对应的扇形圆心角为 　　度；

（3）从所抽取的优秀等级的学生 $A$ 、 $B$ 、 $C\dots$ 中，随机选取两人去参加即将举办的学校运动会，请根据列表或画树状图的方法，求出恰好抽到 $A$ 、 $B$ 两位同学的概率．

为庆祝建党100周年，让同学们进一步了解中国科技的快速发展，东营市某中学九（1）班团支部组织了一次手抄报比赛．该班每位同学从 $A$ ．"北斗卫星"； $B$ ．" $5G$ 时代"； $C$ ．"东风快递"； $D$ ．"智轨快运"四个主题中任选一个自己喜欢的主题．统计同学们所选主题的频数，绘制成不完整的统计图，请根据统计图中的信息解答下列问题：

（1）九（1）班共有 　　名学生；

（2）补全折线统计图；

（3） $D$ 所对应扇形圆心角的大小为 　　；

（4）小明和小丽从 $A$ 、 $B$ 、 $C$ 、 $D$ 四个主题中任选一个主题，请用列表或画树状图的方法求出他们选择相同主题的概率．

经过某路口的汽车，可能直行，也可能左拐或右拐．假设这三种可能性相同，现有两车经过该路口，恰好有一车直行，另一车左拐的概率为 $($ 　　 $)$

A．

$\frac{2}{9}$

B．

$\frac{1}{3}$

C．

$\frac{4}{9}$

D．

$\frac{5}{9}$

为了倡导“节约用水，从我做起”，某市政府决定对该市直属机关200户家庭用水情况进行调查．市政府调查小组随机抽查了其中部分家庭一年的月平均用水量（单位：吨），调查中发现，每户家庭月平均用水量在 $3~7$吨范围内，并将调查结果制成了如下尚不完整的统计表：

月平均用水量（吨 $)$	3	4	5	6	7
频数（户数）	4	$a$	9	10	7
频率	0.08	0.40	$b$	$c$	0.14

请根据统计表中提供的信息解答下列问题：

（1）填空： $a=$　　， $b=$　　， $c=$　　．

（2）这些家庭中月平均用水量数据的平均数是 　　，众数是 　　，中位数是 　　．

（3）根据样本数据，估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户？

（4）市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中，选取两户进行“节水”经验分享．请用列表或画树状图的方法，求出恰好选到甲、丙两户的概率，并列出所有等可能的结果．