为了解甲、乙两座城市的邮政企业4月份收入的情况,从这两座城市的邮政企业中,各随机抽取了25家邮政企业,获得了它们4月份收入(单位:百万元)的数据,并对数据进行整理、描述和分析.下面给出了部分信息.
.甲城市邮政企业4月份收入的数据的频数分布直方图如下(数据分成5组: , , , ,

.甲城市邮政企业4月份收入的数据在 这一组的是:
10.0 10.0 10.1 10.9 11.4 11.5 11.6 11.8
.甲、乙两座城市邮政企业4月份收入的数据的平均数、中位数如下:
平均数 |
中位数 |
|
甲城市 |
10.8 |
|
乙城市 |
11.0 |
11.5 |
根据以上信息,回答下列问题:
(1)写出表中 的值;
(2)在甲城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为 .在乙城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为 .比较 , 的大小,并说明理由;
(3)若乙城市共有200家邮政企业,估计乙城市的邮政企业4月份的总收入(直接写出结果).
2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位: 绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 |
频数 |
|
|
|
12 |
|
|
|
10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中 , ;
(2)样本成绩的中位数落在 范围内;
(3)请把频数分布直方图补充完整;
(4)该校共有1200名学生,估计该学校学生立定跳远成绩在 范围内的有多少人?

在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间 (单位:小时).把调查结果分为四档, 档: ; 档: ; 档: ; 档: .根据调查情况,给出了部分数据信息:
① 档和 档的所有数据是:7,7,7.5,10,7,10,7,7.5,7,7,10.5,10.5;
②图1和图2是两幅不完整的统计图.
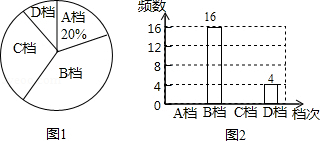
根据以上信息解答问题:
(1)求本次调查的学生人数,并将图2补充完整;
(2)已知全校共1200名学生,请你估计全校 档的人数;
(3)学校要从 档的4名学生中随机抽取2名作读书经验分享,已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.
2020年是脱贫攻坚年.为实现全员脱贫目标,某村贫困户在当地政府支持帮助下,办起了养鸡场.经过一段时间精心饲养,总量为3000只的一批鸡可以出售.现从中随机抽取50只,得到它们质量的统计数据如下:
| 质量 |
组中值 |
频数(只 |
|
|
1.0 |
6 |
|
|
1.2 |
9 |
|
|
1.4 |
|
|
|
1.6 |
15 |
|
|
1.8 |
8 |
根据以上信息,解答下列问题:
(1)表中 ,补全频数分布直方图;
(2)这批鸡中质量不小于 的大约有多少只?
(3)这些贫困户的总收入达到54000元,就能实现全员脱贫目标.按15元 的价格售出这批鸡后,该村贫困户能否脱贫?

某校"校园主持人大赛"结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:

(1)本次比赛参赛选手共有 人,扇形统计图中" "这一范围的人数占总参赛人数的百分比为 ;
(2)补全图2频数直方图;
(3)赛前规定,成绩由高到低前 的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;
(4)成绩前四名是2名男生和2名女生,若从他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.
某学校开展了防疫知识的宣传教育活动.为了解这次活动的效果,学校从全校1500名学生中随机抽取部分学生进行知识测试(测试满分100分,得分 均为不小于60的整数),并将测试成绩分为四个等级:基本合格 ,合格 ,良好 ,优秀 ,制作了如图统计图(部分信息未给出).

由图中给出的信息答案下列问题:
(1)求测试成绩为合格的学生人数,并补全频数直方图.
(2)求扇形统计图中“良好”所对应的扇形圆心角的度数.
(3)这次测试成绩的中位数是什么等级?
(4)如果全校学生都参加测试,请你根据抽样测试的结果,估计该校获得优秀的学生有多少人?
某工厂生产某种产品,3月份的产量为5000件,4月份的产量为10000件.用简单随机抽样的方法分别抽取这两个月生产的该产品若干件进行检测,并将检测结果分别绘制成如图所示的扇形统计图和频数直方图(每组不含前一个边界值,含后一个边界值).已知检测综合得分大于70分的产品为合格产品.
(1)求4月份生产的该产品抽样检测的合格率;
(2)在3月份和4月份生产的产品中,估计哪个月的不合格件数多?为什么?

新冠疫情防控期间,全国中小学开展“停课不停学”活动.某市为了解初中生每日线上学习时长 (单位:小时)的情况,在全市范围内随机抽取了 名初中生进行调查,并将所收集的数据分组整理,绘制了如图所示的不完整的频数分布直方图和扇形统计图.

根据图中信息,解答下列问题:
(1)在这次调查活动中,采取的调查方式是 (填写“全面调查”或“抽样调查” , ;
(2)从该样本中随机抽取一名初中生每日线上学习时长,其恰好在“ ”范围的概率是 ;
(3)若该市有15000名初中生,请你估计该市每日线上学习时长在“ ”范围的初中生有 名.
某鞋店在一周内销售某款女鞋,尺码(单位: 数据收集如下:
24 |
23.5 |
21.5 |
23.5 |
24.5 |
23 |
22 |
23.5 |
23.5 |
23 |
22.5 |
23.5 |
23.5 |
22.5 |
24 |
24 |
22.5 |
25 |
23 |
23 |
23.5 |
23 |
22.5 |
23 |
23.5 |
23.5 |
23 |
24 |
22 |
22.5 |
绘制如图不完整的频数分布表及频数分布直方图:
尺码 |
划记 |
频数 |
|
|
3 |
|
|
|
|
|
13 |
|
|
2 |
(1)请补全频数分布表和频数分布直方图;
(2)若店主要进货,她最应该关注的是尺码的众数,上面数据的众数为 ;
(3)若店主下周对该款女鞋进货120双,尺码在 范围的鞋应购进约多少双?

为积极响应教育部“停课不停学”的号召,某中学组织本校优秀教师开展线上教学,经过近三个月的线上授课后,在五月初复学.该校为了解学生不同阶段学习效果,决定随机抽取八年级部分学生进行两次跟踪测评,第一次是复学初对线上教学质量测评,第二次是复学一个月后教学质量测评.根据第一次测试的数学成绩制成频数分布直方图(图 .

复学一个月后,根据第二次测试的数学成绩得到如下统计表:
成绩 |
|
|
|
|
|
|
|
人数 |
1 |
3 |
3 |
8 |
15 |
|
6 |
根据以上图表信息,完成下列问题:
(1) ;
(2)请在图2中作出两次测试的数学成绩折线图,并对两次成绩作出对比分析(用一句话概述);
(3)某同学第二次测试数学成绩为78分.这次测试中,分数高于78分的至少有 人,至多有 人;
(4)请估计复学一个月后该校800名八年级学生数学成绩优秀 分及以上)的人数.
某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记 分 ,组委会从1000篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
征文比赛成绩频数分布表
分数段 |
频数 |
频率 |
|
38 |
0.38 |
|
|
0.32 |
|
|
|
|
10 |
0.1 |
合计 |
1 |
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中 的值是 ;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.

某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,下面是七年级各班一周收集的可回收垃圾的质量的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量的频数表
组别 |
频数 |
|
2 |
|
|
|
3 |
|
1 |
(1)求 的值;
(2)已知收集的可回收垃圾以0.8元 被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到50元?

为积极创建全国文明城市,某市对某路口的行人交通违章情况进行了20天的调查,将所得数据绘制成如下统计图(图2不完整)

请根据所给信息,解答下列问题:
(1)第7天,这一路口的行人交通违章次数是多少次?这20天中,行人交通违章6次的有多少天?
(2)请把图2中的频数直方图补充完整;(温馨提示:请画在答题卷相对应的图上)
(3)通过宣传教育后,行人的交通违章次数明显减少.经对这一路口的再次调查发现,平均每天的行人交通违章次数比第一次调查时减少了4次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别 |
频数 |
|
8 |
|
12 |
|
|
|
10 |
(1)求 的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在 (含 以上的人数.
