先阅读短文,然后回答短文后面所给出的问题:
对于三个数a、b、c的平均数,最小的数都可以给出符号来表示,我们规定 表示这三个数的平均数,
表示这三个数的平均数,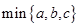 表示这三个数中的最小的数,
表示这三个数中的最小的数, 表示这三个数中最大的数.例如:
表示这三个数中最大的数.例如: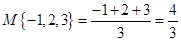 ,
,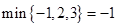 ,
,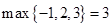 ;
; ,
, .
.
(1)请填空: ;若
;若 ,则
,则 ;
;
(2)若 ,求
,求 的取值范围;
的取值范围;
(3)若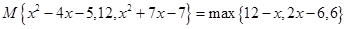 ,求
,求 的值.
的值.
某地因持续高温干旱,村民饮水困难,镇政府组织村民组成水源行动小组到村镇周边找水。某村民在山洞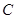 里发现了暗河(如图所示),经勘察,在山洞的西面有一条南北走向的公路连接着
里发现了暗河(如图所示),经勘察,在山洞的西面有一条南北走向的公路连接着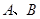 两村庄,山洞
两村庄,山洞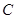 位于
位于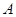 村庄南偏东
村庄南偏东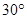 方向,且位于
方向,且位于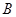 村庄南偏东
村庄南偏东 方向。为方便
方向。为方便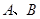 两村庄的村民取水,准备从山洞
两村庄的村民取水,准备从山洞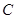 处向公路
处向公路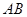 紧急修建一条最近的简易公路
紧急修建一条最近的简易公路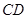 ,现已知
,现已知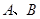 两村庄相距6千米。
两村庄相距6千米。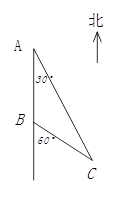
(1)求这条最近的简易公路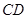 的长(精确到0.1千米)?
的长(精确到0.1千米)?
(2)现由甲、乙两施工队共同合作修建这条公路,已知甲施工队修建2千米后,由乙施工队继续修建,乙施工队每天施工的速度是甲施工队每天施工速度的1.6倍,8天后,公路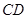 正式通车。求甲、乙两施工队每天修建公路多少千米?
正式通车。求甲、乙两施工队每天修建公路多少千米?
(参考数据: ,
,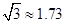 )
)
阅读下面材料:
小明遇到这样一个问题:如图1,在边长为 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.

小明发现:分别延长QE,MF, NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)。请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
(3)参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 ,则AD的长为__________.
,则AD的长为__________.
如图,建筑物AB后有一座假山,其坡度为i=1: ,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
小明家要在卫生间墙壁(AB)上安装一个淋浴装置.要求淋浴头放至插槽中正常情况下使用时,水不能喷洒到对面墙壁(MN)上,小明经过研究和测量,将其简化成下面的问题:已知淋浴头放入插槽后,喷射最远的水线DE与CD的夹角∠CDE=87°,CD=0.2m,∠BCD=45°,两墙壁之间的距离为2m.请计算插槽安装的最大高度AC.(结果精确到0.1米,参考数据: ≈1.41,tan48°≈1.11,tan42°≈0.90)
≈1.41,tan48°≈1.11,tan42°≈0.90)
如图,在一笔直的海岸线l上有A、B两个观测站,A在B的正东方向,BP=3 (单位:km)有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(单位:km)有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向.
(1)求A、B两个观测站之间的距离;
(2)小船从点P处沿射线AP的方向以 千米/时的速度进行沿途考查,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°的方向,求小船沿途考察的时间.(结果有根号的保留根号)
千米/时的速度进行沿途考查,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°的方向,求小船沿途考察的时间.(结果有根号的保留根号)
(本小题满分8分)如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm
(1)若OB=6cm.
①求点C的坐标;
②若点A向右滑动的距离与点B向上滑动的距离相等,求滑动的距离;
(2)点C与点O的距离的最大值.
(本小题满分9分)如图1,已知B点坐标是(6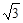 ,6),BA⊥x轴于A,BC⊥y轴于C,D在线段OA上,E在y轴的正半轴上,DE⊥BD,M是DE中点,且M在OB上.
,6),BA⊥x轴于A,BC⊥y轴于C,D在线段OA上,E在y轴的正半轴上,DE⊥BD,M是DE中点,且M在OB上.
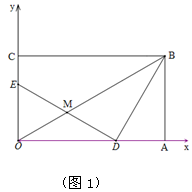
(1)点M的坐标是( , ),DE= ;
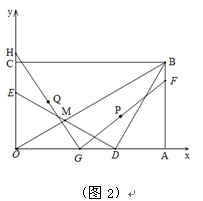
(2)小明在研究动点问题时发现,如果有两点分别在两条互相垂直的直线上做匀速运动,连接这两点所得线段的中点将在同一条直线上运动,利用这一事实解答下列问题,如图2,如果一动点F从点B出发以每秒1个单位长度的速度向点A运动,同时有一点G从点D出发以每秒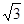 个单位长度的速度向点O运动,点H从点E开始沿y轴正方向自由滑动,并始终保持GH=DE,P为FG的中点,Q为GH的中点,F与G两个点分别运动到各自终点时停止运动,分别求出在运动过程中点P、Q运动的路线长.
个单位长度的速度向点O运动,点H从点E开始沿y轴正方向自由滑动,并始终保持GH=DE,P为FG的中点,Q为GH的中点,F与G两个点分别运动到各自终点时停止运动,分别求出在运动过程中点P、Q运动的路线长.
(3)连接PQ,求当运动多少秒时,PQ最小,最小值是多少?
如图,是一副学生用的三角板,在△ABC 中,∠C=90°,∠A=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠A1=45°,∠B1=45°,且A1B1=CB.若将边A1C1与边CA重合,其中点A1与点C重合.将三角板A1B1C1绕点C(A1)按逆时针方向旋转,旋转过的角为α,旋转过程中边A1C1与边AB的交点为M,设AC=a.
(1)计算A1C1的长;
(2)当α=30°时,证明:B1C1∥AB;
(3)若a= ,当α=45°时,计算两个三角板重叠部分图形的面积;
,当α=45°时,计算两个三角板重叠部分图形的面积;
(4)当α=60°时,用含a的代数式表示两个三角板重叠部分图形的面积.
(参考数据:sin15°= ,cos15°=
,cos15°= ,tan15°=2-
,tan15°=2- ,sin75°=
,sin75°= ,cos75°=
,cos75°= ,tan75°=2+
,tan75°=2+ )
)
如图(1),在矩形ABCD中,AB=6,BC=2 ,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,如图(2)以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t>0).
,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,如图(2)以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t>0).
(1)如图(3),当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)如图(4),当等边△EFG的顶点G恰好落在CD边上时,求运动时间t的值;
(3)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请求出S与t之间的函数关系式,并写出相应的自变量的取值范围.
小锋家有一块四边形形状的空地(如图,四边形ABCD),其中AD∥BC,BC=1.6m,AD=5.5m,CD=5.2m,∠C=90°,∠A=53°.小锋的爸爸想买一辆长4.9m,宽1.9m的汽车停放在这块空地上,让小锋算算是否可行.
小锋设计了两种方案,如图1和图2所示.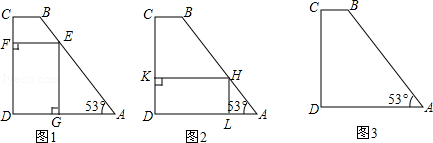
(1)请你通过计算说明小锋的两种设计方案是否合理;
(2)请你利用图3再设计一种有别于小锋的可行性方案,并说明理由.
(参考数据:sin53°=0.8,cos53°=0.6,tan53°= )
)
如图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4米,AB=6米,中间平台宽度DE=1米,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB= ,DF⊥BC于F,∠CDF=
,DF⊥BC于F,∠CDF= .求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin
.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin ≈0.52,cos
≈0.52,cos ≈0.86,tan
≈0.86,tan ≈0.60)
≈0.60)
如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm.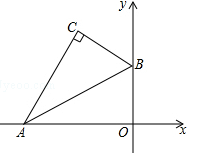
(1)若OB=6cm.
①求点C的坐标;
②若点A向右滑动的距离与点B向上滑动的距离相等,求滑动的距离;
(2)点C与点O的距离的最大值= cm.
如图,一侧面为矩形的建筑物ABCD,AP为建筑物上一灯杆(垂直于地面),夜晚灯杆顶端灯亮时,EH段是建筑物在斜坡EF上的影子.己知BC=8米,AP=12米,CE=6米,斜坡EF的坡角∠FEG=30°,EH=4米,且B,C,E,G在同一水平线上,题中涉及的各点均在同一平面内,求建筑物的高度AB(结果保留根号).
张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据: ≈1.732)
≈1.732)