如图,一侧面为矩形的建筑物ABCD,AP为建筑物上一灯杆(垂直于地面),夜晚灯杆顶端灯亮时,EH段是建筑物在斜坡EF上的影子.己知BC=8米,AP=12米,CE=6米,斜坡EF的坡角∠FEG=30°,EH=4米,且B,C,E,G在同一水平线上,题中涉及的各点均在同一平面内,求建筑物的高度AB(结果保留根号).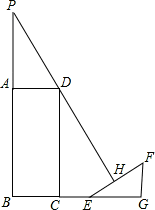
相关知识点
推荐套卷
如图,一侧面为矩形的建筑物ABCD,AP为建筑物上一灯杆(垂直于地面),夜晚灯杆顶端灯亮时,EH段是建筑物在斜坡EF上的影子.己知BC=8米,AP=12米,CE=6米,斜坡EF的坡角∠FEG=30°,EH=4米,且B,C,E,G在同一水平线上,题中涉及的各点均在同一平面内,求建筑物的高度AB(结果保留根号).