小明家要在卫生间墙壁(AB)上安装一个淋浴装置.要求淋浴头放至插槽中正常情况下使用时,水不能喷洒到对面墙壁(MN)上,小明经过研究和测量,将其简化成下面的问题:已知淋浴头放入插槽后,喷射最远的水线DE与CD的夹角∠CDE=87°,CD=0.2m,∠BCD=45°,两墙壁之间的距离为2m.请计算插槽安装的最大高度AC.(结果精确到0.1米,参考数据: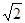 ≈1.41,tan48°≈1.11,tan42°≈0.90)
≈1.41,tan48°≈1.11,tan42°≈0.90)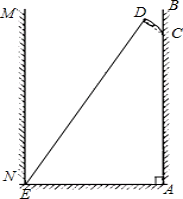
相关知识点
推荐套卷
小明家要在卫生间墙壁(AB)上安装一个淋浴装置.要求淋浴头放至插槽中正常情况下使用时,水不能喷洒到对面墙壁(MN)上,小明经过研究和测量,将其简化成下面的问题:已知淋浴头放入插槽后,喷射最远的水线DE与CD的夹角∠CDE=87°,CD=0.2m,∠BCD=45°,两墙壁之间的距离为2m.请计算插槽安装的最大高度AC.(结果精确到0.1米,参考数据: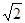 ≈1.41,tan48°≈1.11,tan42°≈0.90)
≈1.41,tan48°≈1.11,tan42°≈0.90)