初中数学解直角三角形选择题

如图1，在4×4的正方形网格中，tanα=    

A．1

B．2

C．

D．

如图是教学用直角三角板，边AC＝30cm，∠C＝90°，
tan∠BAC＝ ，则边BC的长为（■）.

A．cm

B．cm

C．cm

D．cm

如图，在四边形ABCD中，E、F分别是AB、AD的中点。若EF＝2，BC＝5，CD＝3，则tan C等于

A．             B．          C．         D．

在△ABC中，∠C=90°，∠A=72°，AB=10，则边AC的长约为（精确到0.1）（　　）

A．9.1	B．9.5
C．3.1	D．3.5

（11·西宁）某水坝的坡度i＝1:，坡长AB＝20米，则坝的高度为

A．10米

B．20米

C．40米

D．20米

（11·湖州）如图，已知在Rt△ABC中，∠C=90°，BC=1，AC=2，则tanA的
值为

A． 2

B．

C．

D．

如图，已知Rt△ABC中，∠C=90°，BC=3，AC=4，则sinA的值为（　　）

A．	B．
C．	D．

周末，身高都为1.6米的小芳、小丽来到溪江公园，准备用她们所学的知识测算南塔的高度．如图，小芳站在A处测得她看塔顶的仰角a为45°，小丽站在B处（A、B与塔的轴心共线）测得她看塔顶的仰角b为30°．她们又测出A、B两点的距离为30米．假设她们的眼睛离头顶都为10 cm，则可计算出塔高约为（结果精确到0.01，参考数据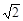：≈1.414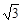，≈1.732）（   ）．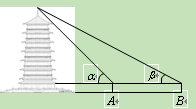

A．36.21米          B．37.71米             C．40.98米             D．42.48米

在一次夏令营活动中，小霞同学从营地点出发，要到距离点的地
去，先沿北偏东方向到达地，然后再沿北偏西方向走了到达目的地,
此时小霞在营地的

A．北偏东方向上	B．北偏东方向上
C．北偏东方向上	D．北偏西方向上

如图，将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下，使木桩向上运动，已知楔子斜面的倾斜角为20°，若楔子沿水平方向前移8cm（如箭头所示），则木桩上升了（　　）

A．8tan20°

B．

C．8sin20°

D．8cos20°

若∠α的余角是30°，则cosα的值是（　　）

A．

B．

C．

D．

（

如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．若AC=，BC=2，则sin∠ACD的值为（　　）

A、               B、
C、               D、

如图，在 $△ABC$ 中， $\angle C=90°$， $BC=6$， $D$， $E$ 分别在 $AB、AC$上，将 $△ABC$沿DE折叠，使点 $A$落在点 $A\prime$处，若 $A\prime$ 为CE的中点，则折痕 $DE$的长为（　　）

A． $\frac{1}{2}$   B． $2$  C． $3$  D． $4$

如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连结DE、EF.下列结论：①tan∠ADB="2 " ②图中有4对全等三角形③若将△DEF沿EF折叠，则点D不一定落在AC上④BD="BF " ⑤S_{四边形DFOE}=S_△AOF，上述结论中正确的个数是（     ）
A  1个           B  2个      C  3个                D  4个