如图,一辆小车沿倾斜角为 的斜坡向上行驶13米,已知 ,则小车上升的高度是

A.5米B.6米C.6.5米D.12米
如图,点 是矩形 的边 上的点, ,将矩形沿着过点 的直线翻折后,点 、 分别落在边 下方的点 、 处,且点 、 、 在同一条直线上,折痕与边 交于点 , 与 交于点 .若 ,那么 的周长为

A. B. C. D.6
如图,正方形 中,点 、 分别在边 , 上, 与 交于点 .若 , ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径 ,根据我国魏晋时期数学家刘徽的"割圆术"思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计 的值,下面 及 的值都正确的是

| A. |
, |
| B. |
, |
| C. |
, |
| D. |
, |
如图, 中, , , 于点 , 是线段 上的一个动点,则 的最小值是

| A. |
|
B. |
|
C. |
|
D. |
10 |
如图, 为平行四边形 边 上一点, 、 分别是 、 (靠近点 的三等分点, 、 、 的面积分别为 、 、 ,若 , , ,则 的值为

A. B. C. D.4
如图,将长、宽分别为 , 的长方形纸片分别沿 , 折叠,点 , 恰好重合于点 .若 ,则折叠后的图案(阴影部分)面积为

| A. |
|
B. |
|
C. |
|
D. |
|
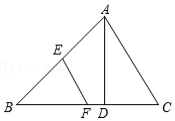
如图,在 中, , , 于点 , .若 , 分别为 , 的中点,则 的长为
| A. |
|
B. |
|
C. |
1 |
D. |
|
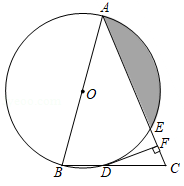
如图,在 中, ,以 为直径的 分别与 , 交于点 , ,过点 作 ,垂足为点 ,若 的半径为 , ,则阴影部分的面积为
| A. |
|
B. |
|
C. |
|
D. |
|
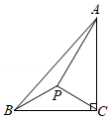
如图, 中, , , .点 为 内一点,且满足 .当 的长度最小时, 的面积是
| A. |
3 |
B. |
|
C. |
|
D. |
|
如图, 、 是 的切线,切点为 、 . 是 的直径, 与 交于点 ,连接 .下列结论:① ② ③若 ,则 ④ ,其中正确结论的个数为

A.4个B.3个C.2个D.1个