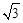初中数学解直角三角形选择题

在△ABC中，若sinA=，则△ABC的形状是（     ）

A．锐角三角形

B．直角三角形

C．钝角三角形

D．不能确定

在△ABC中，∠C=90°，∠A=72°，AB=10，则边AC的长约为（精确到0.1）（　　）

A．9.1	B．9.5
C．3.1	D．3.5

如图，要测量B点到河岸AD的距离，在A点测得∠BAD=30°，在C点测得∠BCD=60°，又测得AC=100米，则B点到河岸AD的距离为（ ）．

A．100米

B．50米

C．米

D．50米

（11·湖州）如图，已知在Rt△ABC中，∠C=90°，BC=1，AC=2，则tanA的
值为

A． 2

B．

C．

D．

小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得 $\angle \mathit{PB}\text{'}C＝\alpha$（B′C为水平线），测角仪B′D的高度为1米，则旗杆PA的高度为（　　）

A． $\frac{1}{1-\sin \alpha }$B． $\frac{1}{1+\sin \alpha }$C． $\frac{1}{1-\cos \alpha }$D． $\frac{1}{1+\cos \alpha }$

如图，Rt△ABC中，∠A=90°，∠ABC=60°，AC=3，点P是边BC上一点，点Q是边AC上一点（不与点A、C重合），且BP=PQ,则BP的取值范围是（  ）

A.     B.     C.     D.

如图，将长、宽分别为 $12\mathit{cm}$ ， $3\mathit{cm}$ 的长方形纸片分别沿 $\mathit{AB}$ ， $\mathit{AC}$ 折叠，点 $M$ ， $N$ 恰好重合于点 $P$ ．若 $\angle \alpha =60°$ ，则折叠后的图案（阴影部分）面积为 $($ 　　 $)$

A．

$(36-6\sqrt{3})c{m}^2$

B．

$(36-12\sqrt{3})c{m}^2$

C．

$24c{m}^2$

D．

$36c{m}^2$

如图，在 $\mathit{\Delta ABC}$ 中， $\angle B=45°$ ， $\angle C=60°$ ， $\mathit{AD}\perp \mathit{BC}$ 于点 $D$ ， $\mathit{BD}=\sqrt{3}$ ．若 $E$ ， $F$ 分别为 $\mathit{AB}$ ， $\mathit{BC}$ 的中点，则 $\mathit{EF}$ 的长为 $($ 　　 $)$

A．

$\frac{\sqrt{3}}{3}$

B．

$\frac{\sqrt{3}}{2}$

C．

1

D．

$\frac{\sqrt{6}}{2}$

如图，在 $\mathit{\Delta ABC}$ 中， $\mathit{AB}=\mathit{AC}$ ，以 $\mathit{AB}$ 为直径的 $\odot O$ 分别与 $\mathit{BC}$ ， $\mathit{AC}$ 交于点 $D$ ， $E$ ，过点 $D$ 作 $\mathit{DF}\perp \mathit{AC}$ ，垂足为点 $F$ ，若 $\odot O$ 的半径为 $4\sqrt{3}$ ， $\angle \mathit{CDF}=15°$ ，则阴影部分的面积为 $($ 　　 $)$

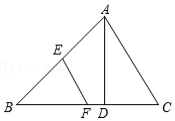
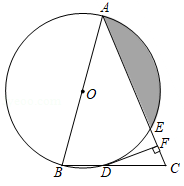
A．

$16\pi -12\sqrt{3}$

B．

$16\pi -24\sqrt{3}$

C．

$20\pi -12\sqrt{3}$

D．

$20\pi -24\sqrt{3}$

如图， $\text{Rt}\Delta \text{ABC}$ 中， $\angle \mathit{ACB}=90°$ ， $\mathit{AC}=2\sqrt{3}$ ， $\mathit{BC}=3$ ．点 $P$ 为 $\mathit{\Delta ABC}$ 内一点，且满足 $P{A}^2+P{C}^2=A{C}^2$ ．当 $\mathit{PB}$ 的长度最小时， $\mathit{\Delta ACP}$ 的面积是 $($ 　　 $)$

A．

3

B．

$3\sqrt{3}$

C．

$\frac{3\sqrt{3}}{4}$

D．

$\frac{3\sqrt{3}}{2}$

如图， $\mathit{PA}$、 $\mathit{PB}$是 $\odot O$的切线，切点为 $A$、 $B$． $\mathit{AC}$是 $\odot O$的直径， $\mathit{OP}$与 $\mathit{AB}$交于点 $D$，连接 $\mathit{BC}$．下列结论：① $\angle \mathit{APB}=2\angle \mathit{BAC}$② $\mathit{OP}//\mathit{BC}$③若 $\tan C=3$，则 $\mathit{OP}=5\mathit{BC}$④ $A{C}^2=4\mathit{OD}·\mathit{OP}$，其中正确结论的个数为 $($　　 $)$

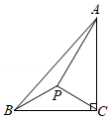
A．4个B．3个C．2个D．1个

如图， $A$、 $B$、 $C$是小正方形的顶点，且每个小正方形的边长为1，则 $\tan \angle \mathit{BAC}$的值为 $($　　 $)$

A． $\frac{1}{2}$B．1C． $\frac{\sqrt{3}}{3}$D． $\sqrt{3}$

在Rt△ABC中，∠C=90°，下列式子必定成立的是（ ）

A．a=c•sinB

B．a=c•cosB

C．a=c•tanB

D．a=c•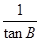

如图，AB是⊙O的直径，AB=4，AC是弦，AC=，∠AOC为（   ）

A．120°

B．130°

C．140°

D．150°

如图，点A、B、O是正方形网格上的三个格点，⊙O的半径为OA，点P是优弧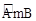上的一点，则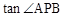的值是【   】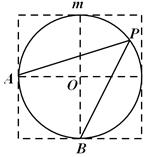

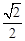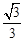A．1    B．      C．     D．