魏朝时期,刘徽利用下图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理.若图中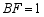 ,
,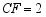 ,则
,则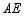 的长为 .
的长为 .
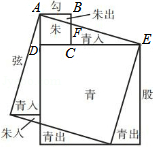
魏朝时期,刘徽利用下图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理.若图中 ,
,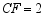 ,则
,则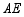 的长为 .
的长为 .

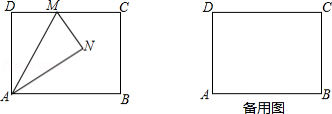
如图,矩形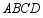 中,
中,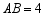 ,
, ,
,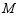 是边
是边 上一点,将
上一点,将 沿直线
沿直线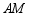 对折,得到
对折,得到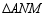 .
.
(1)当 平分
平分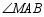 时,求
时,求 的长;
的长;
(2)连接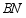 ,当
,当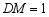 时,求
时,求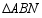 的面积;
的面积;
(3)当射线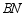 交线段
交线段 于点
于点 时,求
时,求 的最大值.
的最大值.
如图,在 中,
中, ,
,在
,
,在 边上截取
边上截取 ,连接
,连接 .
.
(1)通过计算,判断 与
与 的大小关系;
的大小关系;
(2)求 的度数.
的度数.

如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)

如图,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD于H,点O是AB中点,连接OH,则OH= .

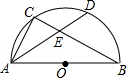
如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为 .
如图,在矩形 中, , ,对角线 , 相交于点 ,点 为边 上一动点,连接 ,以 为折痕,将 折叠,点 的对应点为点 ,线段 与 相交于点 .若 为直角三角形,则 的长为 .

如图,在矩形 中, , ,点 和点 分别为 , 上的点,将 沿 翻折,使点 落在 上的点 处,过点 作 交 于点 ,过点 作 交 于点 .若四边形 与四边形 的面积相等,则 的长为 .

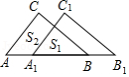
如图,把 沿 边平移到△ 的位置,图中所示的三角形的面积 与四边形的面积 之比为 ,若 ,则此三角形移动的距离 是 .
如图,在 中, ,点 在反比例函数 的图象上,点 , 在 轴上, ,延长 交 轴于点 ,连接 ,若 的面积等于1,则 的值为 .
