初中数学相似多边形的性质填空题

已知菱形ABCD的边长是8，点E在直线AD上，若DE=3，连接BE与对角线AC相交于点M，则的值是             ．

如图是小明设计用手电来测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2米，BP=1.8米，PD=12米，那么该古城墙的高度是 ▲ 米.

如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S_△BDE：S_△CDE=1：3，则S_△DOE：S_△AOC的值为      ．

如图，要使△ADB∽△ABC，还需增添的条件是           （写一个即可）．

如图，E是正方形ABCD的边AB上的动点， EF⊥DE交BC于点F．若正方形的边长为4， AE=，BF=．则 与的函数关系式为          ．

如图，菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在A′、D′处，且A′D′经过B，EF为折痕，当D′F⊥CD时，的值为            ．

为了测量校园水平地面上一棵不可攀的树的高度，学校数学兴趣小组做了如下的探索：根据光的反射定律，利用一面镜子和一根皮尺，设计如图所示的测量方案：把一面很小的镜子放在离树底（B）8.4米的点E处，然后沿着直线BE后退到点D，这时恰好在镜子里看到树梢顶点A，再用皮尺量得DE＝2.4米，观察者目高CD＝1.6米，则树（AB）的高度为            米．

如图，正方形OABC与正方形ODEF是位似图形，点O为位似中心，相似比为1：，点A的坐标为（0，1），则点E的坐标是          ．

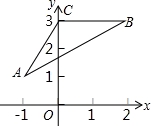
如图，在直角坐标系中，△ABC的各顶点坐标为A（-1，1），B（2，3），C（0，3）．现以坐标原点为位似中心，作△A′B′C′，使△A′B′C′与△ABC的位似比为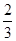．则点A的对应点A′的坐标为                           ．

晚上，小亮走在大街上．他发现：当他站在大街两边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3米，左边的影子长为1．5米．又知自己身高1．80米，两盏路灯的高相同，两盏路灯之间的距离为12米，则路灯的高为           米．

如图，M是△ABC的BC边上的一点，AM的延长线交△ABC的外接圆于D，已知：AD＝12cm， BD＝CD＝6cm，则DM的长为________cm．

如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在A′的位置上．若OB=，，求点A′的坐标为           ．

如图，在△ABC中，D、E分别是AC、AB边上的点，∠AED=∠C，AB=6,AD=4,AC=5,则AE=_______．

如图，已知E、F是平行四边形ABCD对角线BD的三等分点，且CG=5，则AD等于      .

如图，在△ABC中，AB=9，AC=12，BC=18，D为AC上一点，DC=AC．在AB上取一点E得△ADE．若图中两个三角形相似，则DE的长是          ．