初中数学相似多边形的性质选择题

已知△ABC∽△DEF，若△ABC与△DEF的相似比为3：4，则△ABC与△DEF的面积比为（　　）

A．4：3

B．3：4

C．16：9

D．9：16

如果一个三角形能够分成两个与原三角形都相似的三角形，我们把这样的三角形称为孪生三角形，那么孪生三角形是   

A．不存在	B．等腰三角形
C．直角三角形	D．等腰三角形或直角三角形

如图所示，棋盘上有A、B、C三个黑子与P、Q两个白子，要使△ABC ∽△RPQ，则第三个白子R应放的位置可以是 （   ）

A．甲     B．乙     C．丙      D．丁

按如下方法，将△ABC的三边缩小为原来的。如图，任取一点O，连接AO、BO、CO，并取它们的中点D、E、F，得△DEF，则下列说法正确的个数是

(1) △ABC与△DEF是位似图形
(2) △ABC与△DEF是相似图形
(3) △ABC与△DEF的周长比为2∶1
(4) △ABC与△DEF面积比为4∶1
A．4    B．3    C．2     D、1

如图，M是Rt△ABC的斜边BC上异于B、C的一定点，过M点作直线截△ABC，使截得的三角形与△ABC相似，这样的直线共有（　　）

A．1条      B．2条      C．3条      D．4条

给出下列几何图形：
①两个圆；
②两个正方形；
③两个矩形；
④两个正六边形；
⑤两个等腰三角形；
⑥两个直角三角形；
⑦四个角对应相等的两个等腰梯形；
⑧有一个角为40°的菱形．
其中，一定相似的有（ ）个.

A．2

B．3

C．4

D．5

下列关于比例线段和相似的叙述，不正确的是（ ）

A．若 a：b=c：d，则 ac="bd"

B．相似三角形的面积比等于相似比的平方

C．点 C 是线段 AB 的黄金分割点，且AC＞BC，则

D．经过位似多边形对应顶点的直线一定交于同一点

下列多边形一定相似的为（    ）

A．两个三角形

B．两个四边形

C．两个正方形

D．两个平行四边形

如图：在△ABC中，MN∥BC，若BM=4AM，MN=1，则BC的长是（   ）

A．6

B．5

C．4

D．3

如图，能推得DE∥BC的条件是（   ）

A．AD∶AB=DE∶BC

B．AD∶DB=DE∶BC

C．AE∶AC=AD∶DB

D．AD∶DB=AE∶EC

下列各组数中的四条线段能成比例线段的是（   ）

A．a=6，b=4，c=10，d=5

B．a=3，b=7，c=2，d=9

C．a=2，b=4，c=3，d=6

D．a=4，b=11，c=3，d=2

如图，为测量学校旗杆的高度，小东用长为3．2m的竹竿作测量工具，移动竹竿，使竹竿顶端与旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为（  ）m．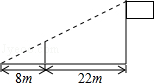

A．8．8

B．10

C．12

D．14

已知,则下列比例式成立的是 (   )

A．

B．

C．

D．

如图，在平行四边形ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BGAE，垂足为G，BG=，则△CEF的周长为（       ）

A．8

B．9.5

C．10

D．11.5

如图，E为平行四边形ABCD的边CB的延长线上一点，DE交AB于点F．则图中与△ADF相似的三角形共有

A．1个

B．2个

C．3个

D．4个