初中数学相似多边形的性质试题

如图，长方形ABCD中，AB=4，AD=3，E是边AB上一点（不与A、B重合），F是边BC上一点（不与B、C重合）．若△DEF和△BEF是相似三角形，则CF=       ．

已知矩形ABCD的一条边AD=8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．

（1）如图，已知折痕与边BC交于点E，连结AP、EP、EA．求证：△ECP∽△PDA；
（2）若△ECP与△PDA的面积比为1：4，求边AB的长；
（3）在（2）的条件下以点A为坐标原点，AB所在直线为x轴，AD所在直线为y轴建立平面直角坐标系，问在坐标平面内是否存在点M，使得以点A、B、E、M为顶点的四边形是平行四边形，若存在请直接写出点M的坐标；若不存在请说明理由。

如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M，N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A，B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM，PN，设移动时间为t（单位：秒，0＜t＜2.5）．

（1）当t为何值时，以A，P，M为顶点的三角形与△ABC相似？
（2）是否存在某一时刻t，使四边形APNC的面积S有最小值？若存在，求S的最小值；若不存在，请说明理由．

（本题8分）如图，四边形ABCD是矩形，直线l垂直平分线段AC，垂足为O，直线l分别与线段AD、CB的延长线交于点E、F．

（1）△ABC与△FOA相似吗？为什么？
（2）试判定四边形AFCE的形状，并说明理由．

如图，矩形纸片ABDC中，AB=5，AC=3，将纸片折叠，使点B落在边CD上的B′处，折痕为AE．在折痕A E上存在一点P到边CD的距离与到点B的距离相等，则此相等距离为__________.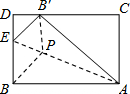

在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN90°．
（1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；
（2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°<α<45°）．
①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；
②如图2，在旋转过程中，当∠DOM15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；
③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD3BP时，猜想此时PE与PF的数量关系，并给出证明；当BDm·BP时，请直接写出PE与PF的数量关系．

如图，已知左右并排的两棵树高分别是AB=8m,CD=12m,两树的根部的距离BD=5m，小明眼睛离地面的高度EF为1.6m，他沿着正对这两棵树的一条水平直路从左到右前进，当他与左边较低的树的距离小于多少时，就不能看到右边较高的树的顶端点C？

如图1，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，边AE上有一动点P（不与A，E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为t秒（0＜t＜5），过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N．

（1）直接写出 D，E 两点的坐标，D（         ），E（           ）
（2）求四边形PMNE的面积S与时间t之间的函数关系式；当t取何值时，S有最大值？
（3）当t为何值时，DP平分∠EDA？
（4）当t为何值时，以A，M，E为顶点的三角形为等腰三角形，并求出相应的时刻点M的坐标．

如图1，正方形纸片ABCD的边长为2，翻折∠B、∠D，使得两个直角的顶点重合于对角线BD上一点P，EF、GH分别是折痕（如图2）．设AE＝x（0＜x＜2），给出下列判断：

①当x＝1时，点P是正方形ABCD的中心；
②当x＝时，EF＋GH＞AC；
③当0＜x＜2时，六边形AEFCHG面积的最大值是；
④当0＜x＜2时，六边形AEFCHG周长的值不变．
其中正确的是________（填序号）．

有两个直角三角板，在三角板ABC中，∠BAC=90°，AB=AC=6，在三角板DEF中，∠FDE=90°，DF=4，DE=4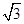，将这两个直角三角板按如图1所示位置摆放，点B与点F重合，直角边BA与FD在同一条直线上．现固定三角板ABC，将三角板DEF沿射线BA方向平行移动，当点F运动到点A时停止运动．
（1）如图2，当三角板DEF运动到点D到点A重合时，设EF与BC交于点M，则∠EMC=        度；
（2）如图3，当三角板DEF运动过程中，当EF经过点C时，求FC的长；
（3）在三角板DEF运动过程中，设BF=x，两块三角板重叠部分的面积为y，求y与x的函数解析式，并求出对应的x取值范围（直接写出结果，不必写过程）．

如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，AC的中点，连接DE．将△EDC绕点C按顺时针方向旋转，记旋转角为α．
（1）问题发现
①当时，；
②当时， 
（2）拓展探究
试判断：当0°≤α＜360°时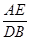，的大小有无变化？请仅就图2的情况给出证明．
（3）问题解决
当△EDC旋转至A、D、E三点共线时，直接写出线段BD的长．

已知△ABC，延长BC到D，使CD=BC．取AB的中点F，连接FD交AC于点E．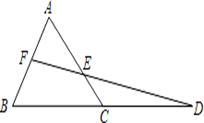

（1）求AE：AC的值；（2）若AB=a，FB=EC，求AC的长．

如图，在平面直角坐标系中，点A、C分别在x轴、y轴上，四边形ABCO为矩形，AB=16，点D与点A关于y轴对称，tan∠ACB=，点E、F分别是线段AD、AC上的动点（点E不与点A、D重合），且∠CEF=∠ACB．

（1）求AC的长和点D的坐标；
（2）说明△AEF与△DCE相似；
（3）当△EFC为等腰三角形时，求点E的坐标．

（年新疆区、兵团12分）如图，直线与x轴交于A点，与y轴交于B点，动点P从A点出发，以每秒2个单位的速度沿AO方向向点O匀速运动，同时动点Q从B点出发，以每秒1个单位的速度沿BA方向向点A匀速运动，当一个点停止运动，另一个点也随之停止运动，连接PQ，设运动时间为t（s）（0＜t≤3）．

（1）写出A，B两点的坐标；
（2）设△AQP的面积为S，试求出S与t之间的函数关系式；并求出当t为何值时，△AQP的面积最大？
（3）当t为何值时，以点A，P，Q为顶点的三角形与△ABO相似，并直接写出此时点Q的坐标．

问题情境：如图1，直角三角板ABC中，∠C＝90°，AC＝BC，将一个用足够长的的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上，再将该直角绕点D旋转，并使其两边分别与三角板的AC边、BC边交于P、Q两点。
问题探究：（1）在旋转过程中，
①如图2，当AD＝BD时，线段DP、DQ有何数量关系？并说明理由。
②如图3，当AD＝2BD时，线段DP、DQ有何数量关系？并说明理由。
③根据你对①、②的探究结果，试写出当AD＝nBD时，DP、DQ满足的数量关系为_______________（直接写出结论，不必证明）
（2）当AD＝BD时，若AB＝20，连接PQ，设△DPQ的面积为S，在旋转过程中，S是否存在最小值或最大值？若存在，求出最小值或最大值；若不存在，请说明理由。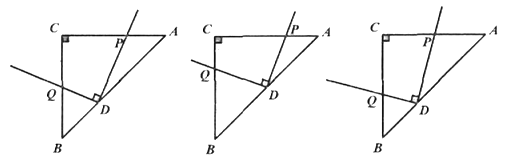

图1              图2                 图3