初中数学相似多边形的性质试题

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．

（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求sinB的值．

如图，M是Rt△ABC的斜边BC上异于B、C的一定点，过M点作直线MN截△ABC交AC于点N，使截得的△CMN与△ABC相似．已知AB=6，AC=8，CM=4，则CN=              ．

如图所示，△ABC中，E、F、D分别是边AB、AC、BC上的点，且满足，则△EFD与△ABC的面积比为        ．

如图所示，在△ABC中D为AC边上一点，若∠DBC=∠A，BC=3，AC=6，则CD的长为（ ）

A．1

B．2

C．

D．

如图，在平面直角系中，直线：分别交轴、轴于、两点，直线分别交轴、轴于、两点，是轴上的一点，，过作轴交于，连接，当动点在线段上运动（不与点点重合）且时

（1）求证：∽；
（2）求线段的长（用的代数式表示）；
（3）若直线的方程是，求tan∠BAC的值．

已知：如图，在梯形ABCD中，AD//BC，∠BCD=90º，对角线AC、BD相交于点E，且AC⊥BD．

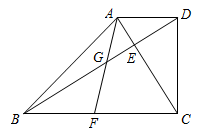
（1）求证：；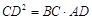
（2）点F是边BC上一点，联结AF，与BD相交于点G．如果∠BAF =∠DBF，求证：．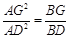

如图，在△中，平分交于点，交于点，，，．求与的长．

已知AD、BE是锐角△ABC的两条高，且AD、BE交于点H，若，则的值为_________．

在△ABC中， 点D、E分别在边AB、AC上，要使，只须添加一个条件， 这个条件可以是：_____________________．（只要填写一种情况）

在△ABC中， 点D在AB上，如果∠ACD=∠B， AD=1， AB="4" ， 那么AC=_________．

在△ABC中， 点D、E分别在边AB、AC上，如果DE//BC， AD：BD=2∶3， 那么DE：BC=_______________．

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B

（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求AE的长．

已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

（1）画出△ABC向下平移4个单位长度得到的△A₁B₁C₁，点C₁的坐标是       ；
（2）以点B为位似中心，在网格内画出△A₂B₂C₂，使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是          ；
（3）△A₂B₂C₂的面积是        平方单位．

如图，在矩形中，点是边的中点，将沿折叠后得到，且点在矩形内部．将延长交边于点．若，则    （用含的代数式表示）．

如图，在等边△ABC中，D，E，F分别是BC，AC，AB上的点，DE⊥AC，EF⊥AB，
FD⊥BC，则△DEF的面积与△ABC的面积之比等于（  ）

A．1∶3

B．2∶3

C．∶2

D．∶3