初中数学相似多边形的性质试题

如图，DF∥AC，DE∥BC，下列各式中正确的是（    ）

A．

B．

C．

D．

如图，在△ABC中，DE∥BC，，则下列结论中正确的是（ ）

A．

B．

C．

D．

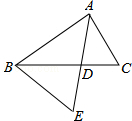
如图，△ABC中，AE交BC于点D，∠C=∠E，AD=4，BC=8，BD：DC=5：3，则DE的长等于（ ）

A．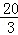

B．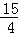

C．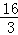

D．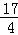

下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（ ）

在平面直角坐标系中，已知点E（﹣4，2），F（﹣2，﹣2），以原点O为位似中心，相似比为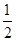，把△EFO缩小，则点E的对应点E′的坐标是（ ）

A．（﹣2，1）	B．（﹣8，4）
C．（﹣2，1）或（2，﹣1）	D．（﹣8，4）或（8，﹣4）

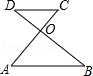
如图，线段AC、BD交于点O，请你添加一个条件：      ，使△AOB∽△COD．

如图，△ABC∽△DEF，相似比为1：2．若BC=1，则EF的长是（  ）

A．1

B．2

C．3

D．4

如图，线段AC、BD交于点O，请你添加一个条件：               ，使△AOB∽△COD．

在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比，已知这本书的长为20cm，则它的宽约为（ ）

A．12．36 cm

B．13．6 cm

C．32．36 cm

D．7．64 cm

如图，小明用长为3m的竹竿CD做测量工具，测量学校旗杆AB的高度，移动竹竿，使竹竿与旗杆的距离DB=12m，则旗杆AB的高为              m．

如图，已知正方形ABCD，点E是边AB上一点，点O是线段AE上的一个动点（不与A、E重合），以O为圆心，OB为半径的圆与边AD相交于点M，过点M作⊙O的切线交DC于点N，连结OM、ON、BM、BN．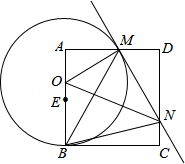

（1）求证：△AOM∽△DMN；
（2）求∠MBN的度数．

如图，为测量学校旗杆的高度，小东用长为3．2m的竹竿作测量工具，移动竹竿，使竹竿顶端与旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为（  ）m．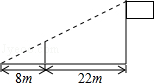

A．8．8

B．10

C．12

D．14

如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABO与△A′B′O′是以点P为位似中心的位似图形，它们的顶点均在格点（网格线的交点）上，则点P的坐标为（ ）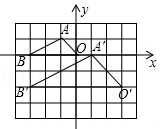

A．（0，0）

B．（0，1）

C．（﹣3，2）

D．（3，﹣2）

如图，线段AB两个端点的坐标分别为A（4，4），B（6，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C和D的坐标分别为（ ）

A．（2，2），（3，2）	B．（2，4），（3，1）
C．（2，2），（3，1）	D．（3，1），（2，2）

如图，点P是▱ABCD边AB上的一点，射线CP交DA的延长线于点E，则图中相似的三角形有（ ）

A．0对

B．1对

C．2对

D．3对