初中数学相似多边形的性质试题

某班某同学要测量学校升旗的旗杆高度，在同一时刻，量得某一同学的身高是1.5m，影长是1m，旗杆的影长是8m，则旗杆的高度是（   ）

A．12m

B．11m

C．10m

D．9m

如图，在△ABC中，∠C=90°,D、E分别为AB、AC边上的两点，且AD·AB=AE·AC,求证：DE⊥AB.

如图，已知O是坐标原点，B、C两点的坐标分别为（3，－1）、（2，1）。
以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2)画出图形。
写出B、C两点的对应点B'、C'的坐标；如果△OBC内部一点M的坐标为(x，y)，写出M的对应点M'的坐标。

如图，给出下列条件：①；②；③；
④其中单独能够判定的个数为（  ）

A．1

B．2

C．3

D．4

如图，小正方形的边长均为1，则图中三角形（粗线）与左图中△ABC相似的是（  ）

如图1，△ABC和△GAF是两个全等的等腰直角三角形，图中相似三角形(不包括全等)共有                                                                               (      )

A．1对	B．2对
C．3对	D．4对

地图上某城市面积为80cm，实际该城市面积为320 km.这地图的比例尺为           

如图，△ABC∽△A′B′C′，AB=3，A′B′=4．若S_△ABC=18，则S_{△A′B′C′}的值为（　　）

A．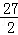

B．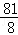

C．24

D．32

已知四条线段a,b,c,d是成比例线段，即＝，下列说法错误的是

A．ad=bc

B．＝

C．＝

D．＝

、若，则            ．

如图，在Rt△ABC中，∠ACB=90º，AB=10，AC=6，点E、F分别是边AC、BC上的动点，过点E作ED⊥AB于点D，过点F作FG⊥AB于点G，DG的长始终为2．
当AD=3时，求DE的长；
当点E、F在边AC、BC上移动时，设，，
求关于的函数解析式，并写出函数的定义域；
在点E、F移动过程中，△AED与△CEF能否相似，
若能，求AD的长；若不能，请说明理由．

如果一个矩形对折后和原矩形相似，则对折后矩形长边与短边的比为  (      )

A．4:1

B．2:1

C．1.5:1

D．:1

在比例尺为的地图上，某建筑物在图上的面积为50 cm²，则该建筑物实际占地面积为

A．50 m^2

B．5000 m^2

C．50000 m^2

D．500000 m^2

已知，则等于

A．2

B．3

C．

D．

如图，已知D、E分别是的AB、AC边上的点，且 
那么等于（   ）

A．1 : 9
B．1 : 3
C．1 : 8
D．1 : 2