(11·湖州)如图,已知A、B是反比例函数 (k>0,x<0)图象上的两
(k>0,x<0)图象上的两
点,BC∥x轴,交y轴于点C。动点P从坐标原点O出发,沿O→A→B→C(图中“→”
所示路线)匀速运动,终点为C。过P作PM⊥x轴,PN⊥y轴,垂足分别为M、N。设四
边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为

如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数 (k≠0)的图象上.
(k≠0)的图象上.
(1)求a的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.
.根据图5中①所示的程序,得到了y与x的函数图象,如图5中②,若点M是
y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P、Q,连接OP、OQ,则以下结论:
①x<0时,y=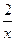
②△OPQ的面积为定值
③x>0时,y随x的增大而增大
④MQ=2PM
⑤∠POQ可以等于90°
其中正确结论是
A.①②④B.②④⑤C.③④⑤D.②③⑤
.如果反比例函数 (k是常数,k≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.
(k是常数,k≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.
如图,在平面直角坐标系xOy中,一次函数y=﹣2x的图象与反比例函数y= 的图象的一个交点为A(﹣1,n).
的图象的一个交点为A(﹣1,n).
(1)求反比例函数y= 的解析式;
的解析式;
(2)若P是坐标轴上一点,且满足PA=OA,直接写出点P的坐标.
在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=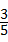 ,反比例函数
,反比例函数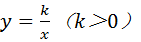 的图象经过AO的中点C,且与AB交于点D,则点D的坐标为____________.
的图象经过AO的中点C,且与AB交于点D,则点D的坐标为____________.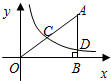
如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.
当点O´与点A重合时,点P的坐标是___________
设P(t,0),当O´B´与双曲线有交点时,t的取值范围是______________
给出下列命题:
命题1:直线 与双曲线
与双曲线 有一个交点是(1,1);
有一个交点是(1,1);
命题2:直线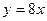 与双曲线
与双曲线 有一个交点是(
有一个交点是( ,4);
,4);
命题3:直线 与双曲线
与双曲线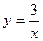 有一个交点是(
有一个交点是( ,9);
,9);
命题4:直线 与双曲线
与双曲线 有一个交点是(
有一个交点是( ,16);
,16);
……………………………………………………
(1)请你阅读、观察上面命题,猜想出命题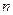 (
(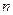 为正整数);
为正整数);
(2)请验证你猜想的命题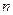 是真命题.
是真命题.
双曲线 、
、 在第一象限的图像如图,
在第一象限的图像如图,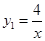 ,过
,过 上的任意一点
上的任意一点 ,作
,作 轴
轴
的平行线交 于
于 ,交
,交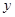 轴于
轴于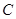 ,若
,若 ,则
,则 的解析式是.
的解析式是.
 |
下列各点中,在反比例函数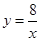 图象上的是
图象上的是
A.(-1,8)B.(-2,4)C.(1,7)D.(2,4)