初中数学平行线分线段成比例试题

甲乙两地相距100km，汽车从甲地开往乙地，所需时间t（小时）和速度v（km/h）之间的函数关系图象大致是下图中（）

若为反比例函数，则m= ( )

A． -4

B．-5

C． 4

D． 5

反比例函数y=的图象位于（）

A．第一、二象限

B．第一、三象限

C．第二、三象限

D．第二、四象限

下列各点中，在函数的图像上的是（）

A．（2，1）

B．（-2，1）

C．（2，-2）

D．（1，2）

如图．直线分别与x轴、y轴交于A、B，与双曲线的图象相交于C、D,其中C（-1，2）

（1）求一次函数解析式.
（2）求反比例函数解析式
（3）若D的坐标为（-2，1）求△OCD的面积
（4）若D的坐标为（-2，1）利用图象直接写出当时x的取值范围

如图，一次函数y1＝kx＋b的图象与反比例函数y2＝的图象交于点A﹙－2，－5﹚，C﹙5，n﹚，

（1）求反比例函数y2＝和一次函数y1＝kx＋b的表达式；
（2）观察图象，写出使函数值的自变量的取值范围

P是反比例函数y＝的图象上一点，过P点分别向x轴、y轴作垂线，所得的图中阴影部分的面积为6，则这个反比例函数的解析式为( )

A．y＝－

B．y＝

C．y＝－

D．y＝

反比例函数y＝的图象位于 -------------------------------------- ( )

A．第一、二象限

B．第一、三象限

C．第二、四象限

D．第三、四象限

如图，一次函数的图象与反比例函数的图象交于点P，点P在第一象限．PA⊥x轴于点A，PB⊥y轴于点B．一次函数的图象分别交轴、轴于点C、D，且S△PBD=4，．

（1）求点D的坐标；
（2）求k、m的值

已知反比例函数的图象经过点A（1，3）．
（1）试确定此反比例函数的解析式；
（2）当=2时, 求y的值；
（3）当自变量从5增大到8时，函数值y是怎样变化的？

如图，已知：双曲线经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为，求点C的坐标．

已知：点在反比例函数的图象上，点B与点A关于坐标轴对称，以AB为边作正方形，则满足条件的正方形的个数是

A．4

B． 5

C． 3

D．8

如图，点A在双曲线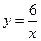上，且OA＝4，过A作AC⊥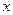轴，垂足为C，OA的垂直平分线交OC于B，则△ABC的周长为( )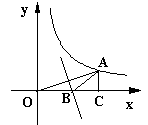

A．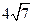

B．5

C．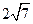

D．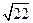

如图，在平面直角坐标系中，反比例函数的图象经过点A（1, 2），B（m ，n）（m＞1），过点B作y轴的垂线,垂足为C.

（1）求该反比例函数解析式；
（2）当△ABC面积为２时，求点B的坐标

给出下列命题：①反比例函数的图象经过一、三象限，且随的增大而减小；②对角线相等且有一个内角是直角的四边形是矩形；③我国古代三国时期的数学家赵爽，创制了一幅“勾股圆方图”，用形数结合得到方法，给出了勾股定理的详细证明（右图）；④相等的弧所对的圆周角相等.其中正确的是（）

A．③④

B．①②③

C．②④

D．①②③④