如图,以O(0,0)、A(2,0)为顶点作正△OAP1,以点P1和线段P1A的中点B为顶点作正△P1BP2,再以点P2和线段P2B的中点C为顶点作△P2CP3,…,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是 .
如图,在平面直角坐标系中,已知点P0坐标为(1,0),将线段OP0绕点O顺时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;将线段OP1绕点O顺时针方向旋转45°,再将其长度伸长为OP1的2倍,得到线段OP2,…,这样依次得到线段OP3,OP4,…,OPn.则点P2的坐标为 ;
当n=4m+1(m为自然数)时,点Pn的坐标为 .
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2),…,根据这个规律,第2015个点的坐标为 .

含60°角的菱形A1B1C1B2,A2B2 C2B3,A3B3C3B4,…,按如图的方式放置在平面直角坐标系xOy中,点A1,A2,A3,…,和点B1,B2,B3,B4,…,分别在直线y=kx和x轴上.已知B1(2,0),B2(4,0),则点A1的坐标是 ;点A3的坐标是 ;点An的坐标是 (n为正整数).
如图,在平面直角坐标系xOy中,已知抛物线(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x 轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x 轴交于另一点A3;将C3绕点A2旋转180°得C4,与x 轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,Cn,….则点A4的坐标为 ;Cn的顶点坐标为 (n为正整数,用含n的代数式表示) .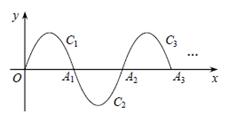
在平面直角坐标系中,A(2,0)、B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰RtAPQ,∠APQ=Rt∠,直线AQ交y轴于点C.

(1)当a=1时,则点Q的坐标为 ;
(2)当点P在直线上运动时,点Q也随之运动.当a= 时,AQ+BQ的值最小为 .
在平面直角坐标系 中,对于点
中,对于点 ,我们把点
,我们把点 叫做点
叫做点 的伴随点,已知点
的伴随点,已知点 的伴随点为
的伴随点为 ,点
,点 的伴随点为
的伴随点为 ,点
,点 的伴随点为
的伴随点为 ,…,这样依次得到点
,…,这样依次得到点 ,
, ,
, ,…,
,…, ,….若点
,….若点 的坐标为(3,1),则点
的坐标为(3,1),则点 的坐标为 ,点
的坐标为 ,点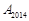 的坐标为 ;若点
的坐标为 ;若点 的坐标为(
的坐标为( ,
, ),对于任意的正整数
),对于任意的正整数 ,点
,点 均在
均在 轴上方,则
轴上方,则 ,
, 应满足的条件为 .
应满足的条件为 .
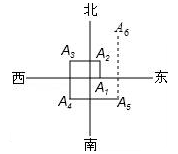
如图,一个机器人从点O出发,向正东方向走3m到达点A1,再向正北方向走6m到达点A2,再向正西方向走9m到达点A3,再向正南方向走12m到达点A4,再向正东方向走15m到达点A5.按如此规律下去,当机器人走到点A6时,离点O的距离是 m.
如图,所有正三角形的一边平行于x轴,一顶点在y轴上.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用 表示,其中x轴与边
表示,其中x轴与边 ,边
,边 与
与 ,
, 与
与 ,…均相距一个单位,则顶点
,…均相距一个单位,则顶点 的坐标为 ;
的坐标为 ; 的坐标为 ;
的坐标为 ; (n为正整数)的坐标为 .
(n为正整数)的坐标为 .
如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,-5),A(4,0),则AD·BC= .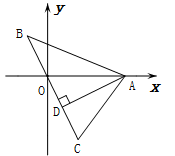
如图,在平面直角坐标系中,⊙O的半径为2,AC、BD是⊙O的两条相互垂直的弦,垂足为M(1, ),则四边形ABCD的面积的最大值与最小值的差为___ ___.
),则四边形ABCD的面积的最大值与最小值的差为___ ___. 
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6…,则顶点A20的坐标为 .
如图,在直角坐标系中,点P0的坐标为( ),将线段OP0绕点O按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1绕点O按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2014的坐标是 .
),将线段OP0绕点O按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1绕点O按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2014的坐标是 .