初中数学坐标与图形变化-旋转解答题

作图题：（不要求定和法）如图，△ABC在平面直角坐标系中，其中，点A、B、C的坐标分别为A（－2，1），B（－4，5），C（－5，2）。

（1）作△ABC关于直线l：x=－1对称的△A₁B₁C₁，其中，点A、B、C的对称点分别为点A₁、B₁、C₁；
（2）写出点A₁、B₁、C₁的坐标。

如图，在方格纸中（小正方形的边长为1），△ABC的三个顶点均为格点，将△ABC沿x轴向左平移5个单位长度，根据所给的直角坐标系（O是坐标原点），解答下列问题：

（1）画出平移后的△A′B′C′，并直接写出点A′、B′、C′的坐标；
（2）求出在整个平移过程中，△ABC扫过的面积．

如图，在平面直角坐标系xOy中，四边形OABC的顶点A在x轴上；∠COA=∠B=60°，且CB∥OA．
（1）求证，四边形OABC是平行四边形．
（2）若A的坐标为（8，0），OC长为6，求点B的坐标．

如图，蚂蚁位于图中点A（2，1）处，按下面的路线移动：（2，1）→（2，4）→（7，4）→（7，7）→（1，7）→（1，1）→（2，1）．请你用线段依次把蚂蚁经过的路线描出来，看看它是什么图案，并括号内写出来．（　    　）

如图，“马”所处的位置为（2，3），其中“马”走的规则是沿着“日”字形的对角线走．
（1）用坐标表示图中“象”的位置是　          　．
（2）写出“马”下一步可以到达的所有位置的坐标．

方格纸中每个小方格都是边长为1个单位长度的正方形，在平面直角坐标系中，已知点A（－4，3）、B（－2，－3）.

（1）描出A、B两点的位置，并连结AB、AO、BO；
（2）△AOB的面积是__________；
（3）把△AOB向右平移4个单位，再向上平移2个单位得到，在图中画出，并写出点、、的坐标.

在平面直角坐标系xOy中，将点A（2，4）向右平移4个单位长度，再向下平移2个单位长度得到点B。
（1）写出点B的坐标；
（2）求出△OAB的面积。

如图，在平面直角坐标系中，A（-1，5），B（-1，0），C（-4，3）．
 
（1）求ΔABC的面积；
（2）在图中画出ΔABC向右平移3个单位，再向下平移2个单位的图形△ABC；
（3）写出点A，B，C的坐标．

如图，已知的三个顶点的坐标分别为A（-2，3）、B（6，0）、C（-1，0）．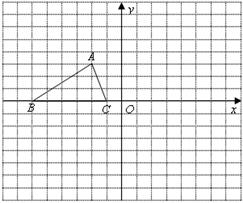

（1）经过怎样的平移，可使的顶点A与坐标原点O重合，并直接写出此时点C的对应点C₁坐标；（不必画出平移后的三角形）
（2）将绕坐标原点O逆时针旋转90°，得到△A′B′C′，画出△A′B′C′.

已知：A（0，1），B（2，0），C（4，3），
（1）求ABC的面积。
（2）设点P在坐标轴上，且ABP与ABC的面积相等，直接写出P的坐标。

如图，在网格图中建立平面直角坐标系，的顶点坐标为、、．

（1）若将向右平移3个单位长度，再向上平移1个单位长度，请画出平移后的；
（2）画出绕C_１顺时针方向旋转90⁰后得到的；
（3）与是中心对称图形，请写出对称中心的坐标：        ；并计算的面积：            .
（4）在坐标轴上是否存在P点，使得△PAB与△CAB的面积相等，若有，则求出点P的坐标.

如图，在平面直角坐标系中，点A，B的坐标分别为A（－1，0）、B（3，0）现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C、D，连接AC，BD．

（1）直接写出点C、D的坐标，求四边形ABDC的面积；
（2）在坐标轴上是否存在一点P，使＝，若存在这样一点，求出点P的坐标，若不存在，试说明理由．
 
（3）如图，在线段CO上取一点G，使OG=3CG，在线段OB上取一点F，使OF=2BF，CF 与BG交于点H，求四边形OGHF的面积.

请在右图中，建立一个平面直角坐标系，使、的坐标分别为(0，1)和(5，)，
       
（1）写出点的坐标；
（2）求三角形ABC的面积．

在某城市中，体育场在火车站以西再往北处，华侨宾馆在火车站以西再往南处，百佳超市在火车站以南再往东，请建立适当的平面直角坐标系，分别写出各地的坐标.（提示：比例尺：一格代表1000m）

如果│3x+3│+│x+3y－2│＝0，那么点P(x，y)在第几象限?