[北京]2012-2013学年北京西城(南区)七年级下学期期末质量检测数学试卷
点(-7,0)位于
| A.x轴正半轴上 | B.y轴负半轴上 |
| C.y轴正半轴上 | D.x轴负半轴上 |
下列长度的三条线段,能组成三角形的是
| A.1cm,2cm,3cm | B.2cm,3cm,6cm |
| C.4cm,6cm,8cm | D.5cm,6cm,12cm |
下列四种调查:
①了解一批炮弹的命中精度; ②调查全国中学生的上网情况;
③审查某文章中的错别字; ④考查某种农作物的长势
其中适合做抽样调查的个数有
| A.1个 | B.2个 | C.3个 | D.4个 |
已知a<b,则下列不等式一定成立的是
| A.a+5>b+5 | B.-2a<-2b | C. |
D.7a-7b<0 |
如果一个多边形的每一个外角都等于40°,那么这个多边形的边数为
| A.9 | B.8 | C.7 | D.6 |
如图,用四个螺丝将四条不可弯曲的木条围成一个木框ABCD,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则现在A、C相对的螺丝的距离的最大值,以及现在B、D相对的螺丝的距离的最大值分别为
A. 5和7 B. 10和7 C. 5和8 D. 10和8
定义:平面内的两条直线l 与l
与l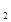 相交于点O,对于该平面内任意一点M,M点到直线l
相交于点O,对于该平面内任意一点M,M点到直线l ,l
,l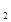 的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”.根据上述定义,“距离坐标”为(2,3)的点的个数是
的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”.根据上述定义,“距离坐标”为(2,3)的点的个数是
| A.1 | B.2 | C.3 | D.4 |
把命题“垂直于同一条直线的两条直线平行”改写成“如果……,那么……”的形式是______________________________________________________.
将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是_____.
如图1,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图2所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为________.
对面积为1的△ABC进行以下操作:分别延长AB、BC、CA至点A 、B
、B 、C
、C ,使得A
,使得A B=2AB,B
B=2AB,B C=2BC,C
C=2BC,C A=2CA,顺次连接A
A=2CA,顺次连接A 、B
、B 、C
、C ,得到△A
,得到△A B
B C
C (如图所示),记其面积为S
(如图所示),记其面积为S .现再分别延长A
.现再分别延长A B
B 、B
、B C
C 、C
、C A
A 至点A
至点A 、B
、B 、C
、C ,使得A
,使得A B
B =2A
=2A B
B ,B
,B C
C =2B
=2B C
C ,C
,C A
A =2C
=2C A
A ,顺次连接A
,顺次连接A 、B
、B 、C
、C ,得到△A
,得到△A B
B C
C ,记其面积为S
,记其面积为S ,则S
,则S =_____________.
=_____________.
先化简,再求值:[(a+b)(a-b)+(a-b) +4a(a+1)]÷2a,其中a=
+4a(a+1)]÷2a,其中a= ,b="-2."
,b="-2."
如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
(1)求ΔABC的面积;
(2)在图中画出ΔABC向右平移3个单位,再向下平移2个单位的图形△A B
B C
C ;
;
(3)写出点A ,B
,B ,C
,C 的坐标.
的坐标.
为了了解初一年级的学生每学期参加综合实践活动的情况,某区教育行政部门随机抽样调查了某校初一年级的学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图.

请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中a的值和该校初一年级学生总数;
(2)求出活动时间为5天的学生人数,并补全条形统计图;
(3)如果某区初一年级的学生共有3000人,根据以上数据,试估计这3000人中“活动时间不少于4天”的百分比.
(1)如图,直线l 、l
、l 分别与直线l
分别与直线l 、l
、l 相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
(2)如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并对此结论进行证明.
如图,在平面直角坐标系中,A(0,1),B(2,0),C(4,3).
(1)求ΔABC的面积;
(2)设点P在坐标轴上,且ΔABP与ΔABC的面积相等,求点P的坐标.
 的解集,正确的是
的解集,正确的是

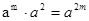


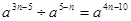
 -x-12=______________.
-x-12=______________. =__________________.
=__________________.
 =(a
=(a ,那么整式M=_______________.
,那么整式M=_______________. y-2x
y-2x y
y -8ax+16a;(2)a
-8ax+16a;(2)a 并写出该不等式组的整数解。
并写出该不等式组的整数解。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号