（1）如图，ΔABC中，∠ABC=50°，∠ACB=70°，D为边BC上一点（D与B、C不重合），连接AD，∠ADB的平分线所在直线分别交直线AB、AC于点E、F. 求证：2∠AED-∠CAD=170°；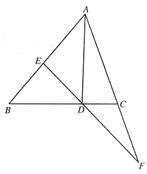
（2）若∠ABC=∠ACB=n°，且D为射线CB上一点，（1）中其他条件不变，请直接写出∠AED与∠CAD的数量关系．（用含n的代数式表示）
相关试题
相关知识点
推荐套卷
（1）如图，ΔABC中，∠ABC=50°，∠ACB=70°，D为边BC上一点（D与B、C不重合），连接AD，∠ADB的平分线所在直线分别交直线AB、AC于点E、F. 求证：2∠AED-∠CAD=170°；
（2）若∠ABC=∠ACB=n°，且D为射线CB上一点，（1）中其他条件不变，请直接写出∠AED与∠CAD的数量关系．（用含n的代数式表示）
粤公网安备 44130202000953号