如图,等腰直角三角形 的直角顶点 与平面直角坐标系的坐标原点 重合, , 分别在坐标轴上, , 在 轴正半轴上沿顺时针方向作无滑动的滚动,在滚动过程中,当点 第一次落在 轴正半轴上时,点 的对应点 的横坐标是

A.2B.3C. D.
如图, 中, , ,将 绕点 逆时针旋转得到 ,使得 ,延长 交 于点 ,则线段 的长为

A.4B.5C.6D.7
如图,将等边 绕点 顺时针旋转 得到 ,连接 , .则下列结论:
① ;② ;③四边形 是菱形.
其中正确的个数是
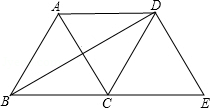
A.0B.1C.2D.3
对于平面图形上的任意两点 , ,如果经过某种变换得到新图形上的对应点 , ,保持 ,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是
A.平移B.旋转C.轴对称D.位似
如图,将矩形 绕点 旋转至矩形 的位置,此时点 恰好与 的中点重合, 交 于点 ,若 ,则 的长为

A.4B. C. D.6
如图,在正方形 中, 为对角线交点,将扇形 绕点 顺时针旋转一定角度得到扇形 ,则在旋转过程中图中阴影部分的面积

A.不变B.由大变小
C.由小变大D.先由小变大,后由大变小
如图, 中, , , , 绕点 顺时针旋转得△ ,当 落在 边上时,连接 ,取 的中点 ,连接 ,则 的长度是

A. B. C.3D.
如图,在 中, , ,在同一平面内,将 绕点 顺时针旋转到△ 的位置,连接 ,若 ,则 的度数是

A. B. C. D.
如图,将 绕点 逆时针旋转 ,得到 ,若点 恰好在 的延长线上,则 的度数为
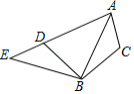
A. B. C. D.
如图,正方形 的对角线相交于点 ,点 , 分别是边 , 上的动点(不与点 , , 重合), , 分别交 于 , 两点,且 ,则下列结论:① ;② ;③ ;④ 是等腰三角形.其中正确的有

A.1个B.2个C.3个D.4个
如图,往竖直放置的在 处由短软管连接的粗细均匀细管组成的“ ”形装置中注入一定量的水,水面高度为 ,现将右边细管绕 处顺时针方向旋转 到 位置,则 中水柱的长度约为
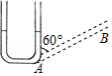
A. B. C. D.
如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点 是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段 绕三角形顶点顺时针转过的角度是

A. B. C. D.
如图,在正方形 中,点 , 分别在 , 上,且 ,将 绕点 顺时针旋转 ,使点 落在点 处,则下列判断不正确的是

A. 是等腰直角三角形B. 垂直平分
C.△ D.△ 是等腰三角形
如图,矩形 绕点 逆时针旋转 后得到矩形 , 与 交于点 ,延长 交 于 ,若 , ,则 的长度为

A. B. C. D.