把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )

A.内部B.外部
C.边上D.以上都有可能
如图,将正方形  中的阴影三角形绕点
中的阴影三角形绕点  顺时针旋转
顺时针旋转  后,得到的图形为
后,得到的图形为 


| A. |
|
B. |
|
C. |
|
D. |
|
下列图形绕某一点旋转一定角度都能与原图形重合,其中旋转角度最小的是
| A. |
|
B. |
|
| C. |
|
D. |
|
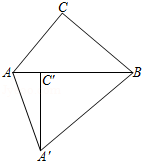
如图, 中, , .将 绕点 逆时针旋转得到△ ,使点 的对应点 恰好落在边 上,则 的度数是
| A. |
|
B. |
|
C. |
|
D. |
|
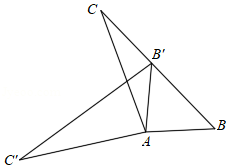
如图,在 中, ,将 绕点 按逆时针方向旋转得到△ .若点 恰好落在 边上,且 ,则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|
如图所示,点 、 、 对应的刻度分别为0、2、4、将线段 绕点 按顺时针方向旋转,当点 首次落在矩形 的边 上时,记为点 ,则此时线段 扫过的图形的面积为

| A. |
|
B. |
6 |
C. |
|
D. |
|
如图,点 在正方形 的边 上,将 绕点 顺时针旋转 到 的位置,连接 ,过点 作 的垂线,垂足为点 ,与 交于点 .若 , ,则 的长为

| A. |
|
B. |
|
C. |
4 |
D. |
|
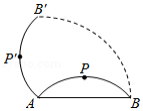
如图,已知 的半径为5,所对的弦 长为8,点 是 的中点,将 绕点 逆时针旋转 后得到 ,则在该旋转过程中,点 的运动路径长是
| A. |
|
B. |
|
C. |
|
D. |
|
下列命题是假命题的是
| A. |
到线段两端点距离相等的点在线段的垂直平分线上 |
| B. |
等边三角形既是轴对称图形,又是中心对称图形 |
| C. |
边形 的内角和是 |
| D. |
旋转不改变图形的形状和大小 |
如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形 的面积为20, ,则 的长为

| A. |
4 |
B. |
|
C. |
6 |
D. |
|
如图,在等腰直角三角形 中, ,一个三角尺的直角顶点与 边的中点 重合,且两条直角边分别经过点 和点 ,将三角尺绕点 按顺时针方向旋转任意一个锐角,当三角尺的两直角边与 , 分别交于点 , 时,下列结论中错误的是

| A. |
|
B. |
|
| C. |
|
D. |
|
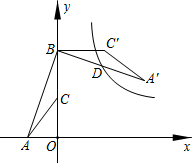
如图,点 的坐标是 ,点 的坐标是 , 为 的中点,将 绕点 逆时针旋转 后得到△ .若反比例函数 的图象恰好经过 的中点 ,则 的值是
| A. |
9 |
B. |
12 |
C. |
15 |
D. |
18 |
如图,四边形 是边长为5的正方形, 是 上一点, ,将 绕着点 顺时针旋转到与 重合,则
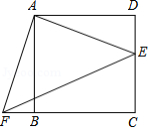
| A. |
|
B. |
|
C. |
|
D. |
|