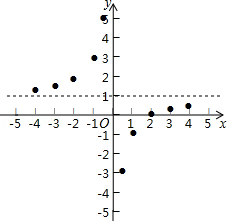如图,在平面直角坐标系中,点 , 在 轴上,点 的坐标为 , .将 先绕点 顺时针旋转 ,再向右平移3个单位长度,则变换后点 的对应点坐标是

A. B. C. D.
如图,把 经过一定的变换得到△ ,如果 上任意一点 的坐标为 ,那么点 在△ 中的对应点 的坐标为 .

如图,线段 经过平移得到线段 ,其中点 , 的对应点分别为点 , ,这四个点都在格点上.若线段 上有一个点 ,则点 在 上的对应点 的坐标为

A. B. C. D.
在平面直角坐标系 中,线段 的两个端点坐标分别为 , ,平移线段 ,得到线段 ,已知 的坐标为 ,则点 的坐标为
A. B. C. D.
将直角三角板 按如图1放置,直角顶点 与坐标原点重合,直角边 、 分别与 轴和 轴重合,其中 .将此三角板沿 轴向下平移,当点 平移到原点 时运动停止.设平移的距离为 ,平移过程中三角板落在第一象限部分的面积为 , 关于 的函数图象(如图2所示)与 轴相交于点 , ,与 轴相交于点 .
(1)试确定三角板 的面积;
(2)求平移前 边所在直线的解析式;
(3)求 关于 的函数关系式,并写出 点的坐标.

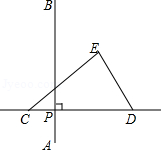
如图,在平面内,线段 , 为线段 上的动点,三角形纸片 的边 所在的直线与线段 垂直相交于点 ,且满足 .若点 沿 方向从点 运动到点 ,则点 运动的路径长为 .
如图,把函数 的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数 的图象;也可以把函数 的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数 的图象.
类似地,我们可以认识其他函数.
(1)把函数 的图象上各点的纵坐标变为原来的 倍,横坐标不变,得到函数 的图象;也可以把函数 的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数 的图象.
(2)已知下列变化:①向下平移2个单位长度;②向右平移1个单位长度;③向右平移 个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的 倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.
(Ⅰ)函数 的图象上所有的点经过④ ② ①,得到函数 的图象;
(Ⅱ)为了得到函数 的图象,可以把函数 的图象上所有的点 .
.① ⑤ ③ .① ⑥ ③ .① ② ⑥ .① ③ ⑥
(3)函数 的图象可以经过怎样的变化得到函数 的图象?(写出一种即可)

在平面直角坐标系中,将点 向下平移2个单位长度,得到的点 的坐标为
A. B. C. D.
如图,直线 与 轴交于点 ,以 为斜边在 轴上方作等腰直角三角形 ,将 沿 轴向右平移,当点 落在直线 上时,则 平移的距离是 .

已知点 的坐标为 ,点 的坐标为 .将线段 沿某一方向平移后,点 的对应点的坐标为 .则点 的对应点的坐标为
A. B. C. D.
如图, 为坐标原点, 是等腰直角三角形, ,点 的坐标为 , ,将该三角形沿 轴向右平移得到 △ ,此时点 的坐标为 , ,则线段 在平移过程中扫过部分的图形面积为 .

在平面直角坐标系中,将点 向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点 的坐标是 .
参照学习函数的过程与方法,探究函数 的图象与性质.
因为 ,即 ,所以我们对比函数 来探究.
列表:
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
1 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
2 |
3 |
5 |
|
|
0 |
|
|
|
描点:在平面直角坐标系中,以自变量 的取值为横坐标,以 相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把 轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当 时, 随 的增大而 ;(填“增大”或“减小”
② 的图象是由 的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3)设 , , , 是函数 的图象上的两点,且 ,试求 的值.