如果三角形的两个内角 与 满足 ,那么我们称这样的三角形为“准互余三角形”.
(1)若 是“准互余三角形”, , ,则 ;
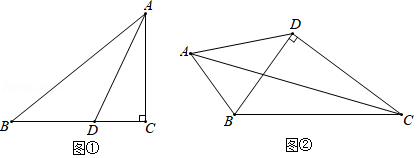
(2)如图①,在 中, , , .若 是 的平分线,不难证明 是“准互余三角形”.试问在边 上是否存在点 (异于点 ,使得 也是“准互余三角形”?若存在,请求出 的长;若不存在,请说明理由.
(3)如图②,在四边形 中, , , , ,且 是“准互余三角形”,求对角线 的长.
如图,把 沿 翻折得 .
(1)连接 ,则 与 的位置关系是 .
(2)不在原图中添加字母和线段,只加一个条件使四边形 是平行四边形,写出添加的条件,并说明理由.

如图, 是 的 边上一点,连接 ,作 的外接圆,将 沿直线 折叠,点 的对应点 落在 上.
(1)求证: .
(2)若 , , ,求 的长.

如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , .将 沿直线 折叠,得到△ ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是

A.
B.△ 的周长是一个定值
C.四边形 的面积是一个定值
D.四边形 的面积是一个定值
如图,将矩形 沿 折叠,点 落在点 处,点 落在 边上的点 处,若 ,则 等于
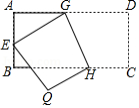
A. B. C. D.
如图,已知在 中, ,点 为 的中点,点 在 上,将 沿 折叠,使得点 恰好落在 的延长线上的点 处,连接 ,则下列结论不一定正确的是
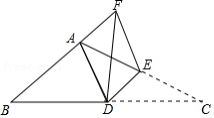
A. B.
C. 和 的面积相等D. 和 的面积相等
折叠矩形纸片 时,发现可以进行如下操作:①把 翻折,点 落在 边上的点 处,折痕为 ,点 在 边上;②把纸片展开并铺平;③把 翻折,点 落在线段 上的点 处,折痕为 ,点 在 边上,若 , ,则 .

如图,矩形 的四个顶点分别在菱形 的四条边上, .将 , 分别沿边 , 折叠,当重叠部分为菱形且面积是菱形 面积的 时,则 为
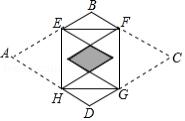
A. B.2C. D.4
如图,矩形纸片 中, , ,将 沿 折叠,使点 落在点 处, 交 于点 ,则 的长等于

A. B. C. D.
如图,在菱形纸片 中, , ,将菱形纸片翻折,使点 落在 的中点 处,折痕为 ,点 , 分别在边 , 上,则 的值为 .
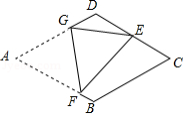
如图1,将 纸片沿中位线 折叠,使点 对称点 落在 边上,再将纸片分别沿等腰 和等腰 的底边上的高线 , 折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.

(1)将 纸片按图2的方式折叠成一个叠合矩形 ,则操作形成的折痕分别是线段 , ; .
(2) 纸片还可以按图3的方式折叠成一个叠合矩形 ,若 , ,求 的长;
(3)如图4,四边形 纸片满足 , , , , ,小明把该纸片折叠,得到叠合正方形,请你帮助画出叠合正方形的示意图,并求出 、 的长.
一块竹条编织物,先将其按如图所示绕直线 翻转 ,再将它按逆时针方向旋转 ,所得的竹条编织物是

A. B.
B.
C. D.
D.
一张矩形纸片 ,已知 , ,小明按如图步骤折叠纸片,则线段 长为

A. B. C.1D.2
如图,一张三角形纸片 ,其中 , , .现小林将纸片做三次折叠:第一次使点 落在 处;将纸片展平做第二次折叠,使点 落在 处;再将纸片展平做第三次折叠,使点 落在 处.这三次折叠的折痕长依次记为 , , ,则 , , 的大小关系是

A. B. C. D.