初中数学扇形面积的计算选择题

如图，从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC，使点A，B，C在圆周上，将剪下的扇形作为一个圆锥的侧面，则这个圆锥的底面圆的半径是（　　）

A． $12\mathit{cm}$B． $6\mathit{cm}$C． $3\sqrt{2}\text{cm}$D． $2\sqrt{3}\text{cm}$

如图，在△ ABC中， AB＝ AC，∠ ABC＝45°，以 AB为直径的⊙ O交 BC于点 D，若 BC＝4 $\sqrt{2}$ ，则图中阴影部分的面积为（　　）

A．

π+1

B．

π+2

C．

2π+2

D．

4π+1

如图，Rt△ ABC中，∠ ACB＝90°，在以 AB的中点 O为坐标原点， AB所在直线为 x轴建立的平面直角坐标系中，将△ ABC绕点 B顺时针旋转，使点 A旋转至 y轴的正半轴上的 A′处，若 AO＝ OB＝1，则阴影部分面积为（　　）

A．

$\frac{2}{3}$ π

B．

$\frac{2}{3}$ π﹣1

C．

$\frac{\pi }{3}$ +1

D．

$\frac{\pi }{3}$

如图，Rt△ABC中，∠ACB＝90°，在以AB的中点O为坐标原点，AB所在直线为x轴建立的平面直角坐标系中，将△ABC绕点B顺时针旋转，使点A旋转至y轴的正半轴上的A′处，若AO＝OB＝1，则阴影部分面积为（　　）

A． $\frac{2}{3}$πB． $\frac{2}{3}$π﹣1C． $\frac{\pi }{3}$+1D． $\frac{\pi }{3}$

如图， AB是⊙ O的直径， CD⊥ AB，∠ ABD＝60°， CD＝2 $\sqrt{3}$ ，则阴影部分的面积为（　　）

A．

$\frac{2}{3}\pi$

B．

π

C．

2π

D．

4π

如图，四边形 ABCD是⊙ O的内接四边形，∠ ABC＝2∠ D，∠ AOB＝ $\frac{1}{3}$ ∠ COB，⊙ O的半径为 $\sqrt{3}$ ，连接 AC交 OB于点 E， OB与 AC相交于点 E，则图中阴影部分面积是（　　）

A．

A $\frac{3\pi }{4}-\frac{3}{2}$

B．

$\frac{\sqrt{3}\pi }{4}-\frac{\sqrt{3}}{2}$

C．

$\frac{3\pi }{4}-\frac{\sqrt{3}}{2}$

D．

$\frac{\sqrt{3}\pi }{4}-\sqrt{3}$

如图，⊙ O的半径为1，分别以⊙ O的直径 AB上的两个四等分点 O ₁， O ₂为圆心， 为半径作圆，则图中阴影部分的面积为（　　）

A．

π

B．

$\frac{1}{2}$ π

C．

$\frac{1}{4}$ π

D．

2π

如图，在Rt△AOB中，∠AOB＝90°，OA＝3，OB＝2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是（　　）

A．πB． $\frac{5\pi }{4}$C．3+πD．8﹣π

如图，点A在以BC为直径的⊙O内，且AB＝AC，以点A为圆心，AC长为半径作弧，得到扇形ABC，剪下扇形ABC围成一个圆锥（AB和AC重合），若∠BAC＝120°， $\mathit{BC}=2\sqrt{3}$，则这个圆锥底面圆的半径是（　　）

A． $\frac{\text{1}}{3}$B． $\frac{\text{2}}{3}$C． $\sqrt{\text{2}}$D． $\sqrt{3}$

如图，把八个等圆按相邻两两外切摆放，其圆心连线构成一个正八边形，设正八边形内侧八个扇形（无阴影部分）面积之和为S₁，正八边形外侧八个扇形（阴影部分）面积之和为S₂，则 $\frac{{\text{S}}_1}{{\text{S}}_2}$＝（　　）

A． $\frac{3}{4}$B． $\frac{3}{5}$C． $\frac{2}{3}$D．1

如图，在扇形 AOB中∠ AOB＝90°，正方形 CDEF的顶点 C是 $\stackrel{̂}{\mathit{AB}}$ 的中点，点 D在 OB上，点 E在 OB的延长线上，当正方形 CDEF的边长为2 时，则阴影部分的面积为（　　）

A．

2π﹣4

B．

4π﹣8

C．

2π﹣8

D．

4π﹣4

如图，半径为10的扇形 $\mathit{AOB}$ 中， $\angle \mathit{AOB}=90°$ ， $C$ 为 $\stackrel{̂}{\mathit{AB}}$ 上一点， $\mathit{CD}\perp \mathit{OA}$ ， $\mathit{CE}\perp \mathit{OB}$ ，垂足分别为 $D$ 、 $E$ ．若 $\angle \mathit{CDE}$ 为 $36°$ ，则图中阴影部分的面积为 $($ 　　 $)$

A．

$10\pi$

B．

$9\pi$

C．

$8\pi$

D．

$6\pi$

如图，在扇形 $\mathit{OAB}$ 中，已知 $\angle \mathit{AOB}=90°$ ， $\mathit{OA}=\sqrt{2}$ ，过 $\stackrel{̂}{\mathit{AB}}$ 的中点 $C$ 作 $\mathit{CD}\perp \mathit{OA}$ ， $\mathit{CE}\perp \mathit{OB}$ ，垂足分别为 $D$ 、 $E$ ，则图中阴影部分的面积为 $($ 　　 $)$

A．

$\pi -1$

B．

$\frac{\pi }{2}-1$

C．

$\pi -\frac{1}{2}$

D．

$\frac{\pi }{2}-\frac{1}{2}$

如图所示，点 $A$ 、 $B$ 、 $C$ 对应的刻度分别为0、2、4、将线段 $\mathit{CA}$ 绕点 $C$ 按顺时针方向旋转，当点 $A$ 首次落在矩形 $\mathit{BCDE}$ 的边 $\mathit{BE}$ 上时，记为点 $A_1$ ，则此时线段 $\mathit{CA}$ 扫过的图形的面积为 $($ 　　 $)$

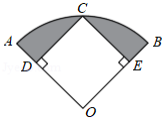
A．

$4\pi$

B．

6

C．

$4\sqrt{3}$

D．

$\frac{8}{3}\pi$

如图，在 $\odot O$ 中， $\mathit{OA}=2$ ， $\angle C=45°$ ，则图中阴影部分的面积为 $($ 　　 $)$

A．

$\frac{\pi }{2}-\sqrt{2}$

B．

$\pi -\sqrt{2}$

C．

$\frac{\pi }{2}-2$

D．

$\pi -2$