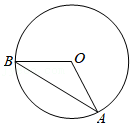
如图,公园内有一个半径为18米的圆形草坪,从 A地走到 B地有观赏路(劣弧 AB)和便民路(线段 AB).已知 A、 B是圆上的点, O为圆心, ,小强从 A走到 B,走便民路比走观赏路少走( )米.
| A. |
|
B. |
|
C. |
|
D. |
|
抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图, , 分别与 相切于点 , ,延长 , 交于点 .若 , 的半径为 ,则图中 的长为 .(结果保留

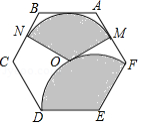
如图,点 为正六边形 的中心,点 为 中点,以点 为圆心,以 的长为半径画弧得到扇形 ,点 在 上;以点 为圆心,以 的长为半径画弧得到扇形 ,把扇形 的两条半径 , 重合,围成圆锥,将此圆锥的底面半径记为 ;将扇形 以同样方法围成的圆锥的底面半径记为 ,则 .
如图,点 的坐标为 ,过点 作 轴的垂线交直线 于点 ,以原点 为圆心, 的长为半径画弧交 轴正半轴于点 ;再过点 作 轴的垂线交直线 于点 ,以原点 为圆心,以 的长为半径画弧交 轴正半轴于点 ; .按此作法进行下去,则 的长是 .

问题:已知 、 均为锐角, , ,求 的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为 ,请借助这个网格图求出 的度数;
延伸:(2)设经过图中 、 、 三点的圆弧与 交于 ,求 的弧长.

如图,已知 是 的内接三角形, 是 的直径,连结 , 平分 .
(1)求证: ;
(2)若 ,求 的长.
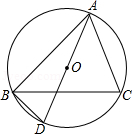
如图, 的直径 ,弦 , 的平分线交 于 ,过点 作 交 的延长线于点 ,连接 , .
(1)由 , , 围成的曲边三角形的面积是 ;
(2)求证: 是 的切线;
(3)求线段 的长.

如图,在扇形 中, , 平分 交 于点 ,点 为半径 上一动点.若 ,则阴影部分周长的最小值为 .

如图, 的半径为3,四边形 内接于 ,连接 、 ,若 ,则劣弧 的长为

A. B. C. D.
如图①,在钝角 中, , ,点 为边 中点,点 为边 中点,将 绕点 逆时针方向旋转 度 .
(1)如图②,当 时,连接 、 .求证: ;
(2)如图③,直线 、 交于点 .在旋转过程中, 的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;
(3)将 从图①位置绕点 逆时针方向旋转 ,求点 的运动路程.
