如图, 为等腰 的外接圆,直径 , 为弧 上任意一点(不与 , 重合),直线 交 延长线于点 , 在点 处切线 交 于点 ,下列结论正确的是 .(写出所有正确结论的序号)
①若 ,则弧 的长为 ;②若 ,则 平分 ;
③若 ,则 ;④无论点 在弧 上的位置如何变化, 为定值.

问题:已知 、 均为锐角, , ,求 的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为 ,请借助这个网格图求出 的度数;
延伸:(2)设经过图中 、 、 三点的圆弧与 交于 ,求 的弧长.

如图,已知 是 的内接三角形, 是 的直径,连结 , 平分 .
(1)求证: ;
(2)若 ,求 的长.
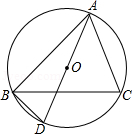
如图,半圆的圆心为 ,直径 的长为12, 为半圆上一点, , 的长是

A. B. C. D.
如图, 的直径 ,弦 , 的平分线交 于 ,过点 作 交 的延长线于点 ,连接 , .
(1)由 , , 围成的曲边三角形的面积是 ;
(2)求证: 是 的切线;
(3)求线段 的长.

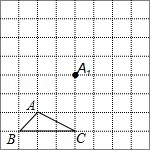
如图所示,正方形网格中, 为格点三角形(即三角形的顶点都在格点上)
①把 沿 方向平移,请在网格中画出当点 移动到点 时的△ ;
②把△ 绕点 按逆时针方向旋转 后得到△ ,如果网格中小正方形的边长为1,求点 旋转到 的路径长.
抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图, , 分别与 相切于点 , ,延长 , 交于点 .若 , 的半径为 ,则图中 的长为 .(结果保留

如图, 的半径是2,扇形 的圆心角为 .若将扇形 剪下围成一个圆锥,则此圆锥的底面圆的半径为 .

如图,在 的正方形网格中,每个小正方形的边长都为1,若将 绕点 顺时针旋转 得到△ ,则 点运动的路径 的长为

A. B. C. D.
(材料阅读)
地球是一个球体,任意两条相对的子午线都组成一个经线圈(如图1中的 .人们在北半球可观测到北极星,我国古人在观测北极星的过程中发明了如图2所示的工具尺(古人称它为“复矩”),尺的两边互相垂直,角顶系有一段棉线,棉线末端系一个铜锤,这样棉线就与地平线垂直.站在不同的观测点,当工具尺的长边指向北极星时,短边与棉线的夹角 的大小是变化的.
(实际应用)
观测点 在图1所示的 上,现在利用这个工具尺在点 处测得 为 ,在点 所在子午线往北的另一个观测点 ,用同样的工具尺测得 为 . 是 的直径, .
(1)求 的度数;
(2)已知
,求这两个观测点之间的距离即
上
的长.
取
