如图, 是等边 的内切圆,分别切 , , 于点 , , , 是 上一点,则 的度数是
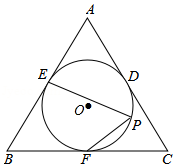
A. B. C. D.
如图,矩形 中, 是 的中点,过 、 、 三点的圆 与边 、 分别交于点 、点 ,给出下列说法:(1) 与 的交点是圆 的圆心;(2) 与 的交点是圆 的圆心;(3) 与圆 相切,其中正确说法的个数是

A.0B.1C.2D.3
如图,四边形 内接于 ,点 是 的内心, ,点 在 的延长线上,则 的度数为
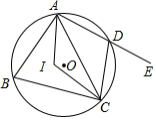
A. B. C. D.
如图,在平面直角坐标系 中, , , , 是 的内心,将 绕原点逆时针旋转 后, 的对应点 的坐标为
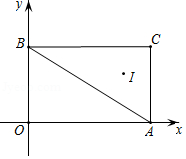
A. B. C. D.
《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”

A.3步B.5步C.6步D.8步
如图,矩形 中, , ,连接 , 和 分别是 和 的内切圆,则 的长是

A. B. C. D.
如图,矩形 中, , ,连接 , 和 分别是 和 的内切圆,则 的长是

A. B. C. D.
如图,在 中, , ,点 是 边上的一点, ,设 与 的内切圆半径分别为 , ,那么

A.2B. C. D.
如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( )

A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI重合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
如图,△ ABC是一块绿化带,将阴影部分修建为花圃,已知 AB=15, AC=9, BC=12,阴影部分是△ ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )

| A. |
|
B. |
|
C. |
|
D. |
|