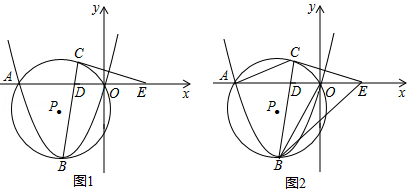
如图1, 是 的直径, 是 延长线上一点, 切 于点 , 交 于点 ,交 的延长线于点 .
(1)求证: 是等腰三角形;
(2) 于 点,交 于 点,过 点作 ,交 于点 ,交 于 点,连接 ,如图2,若 , ,求 的值.

在平面直角坐标系中,已知点 A(﹣2,0), B(2,0), C(3,5).
(1)求过点 A, C的直线解析式和过点 A, B, C的抛物线的解析式;
(2)求过点 A, B及抛物线的顶点 D的⊙ P的圆心 P的坐标;
(3)在抛物线上是否存在点 Q,使 AQ与⊙ P相切,若存在请求出 Q点坐标.

如图,  是
是  的直径,
,
的直径,
,  ,连接
,连接  .
.
(1)求证:  ;
;
(2)若直线  为
为  的切线,
的切线,  是切点,在直线
是切点,在直线  上取一点
上取一点  ,使
,使  ,
,  所在的直线与
所在的直线与  所在的直线相交于点
所在的直线相交于点  ,连接
,连接  .
.
①试探究  与
与  之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 是否为定值?若是,请求出这个定值;若不是,请说明理由.

如图,抛物线 经过点 和点 与 轴的另一交点为点 ,点 是直线 上一动点,过点 作 轴,交抛物线于点 .
(1)求该抛物线的解析式;
(2)在抛物线上是否存在一点 ,使得 是等边三角形?若存在,求出点 的坐标;若不存在,请说明理由;
(3)以 为圆心, 为半径作 ,当 与坐标轴相切时,求出 的半径.

如图,抛物线为常数,
与
轴交于
,
两点,点
为抛物线的顶点,点
的坐标为
,
,连接
并延长与过
,
,
三点的
相交于点
.
(1)求点的坐标;
(2)过点作
的切线
交
轴于点
.
①如图1,求证:;
②如图2,连接,
,
,当
,
时,求
的值.