初中数学圆内接四边形的性质填空题

如图，四边形内接于，，连接，点是半径上任意一点，连接，，则可能为　　度（写出一个即可）．

△ABC中，∠A=50°，高BE、CF所在的直线交于点O，∠BOC的度数是      ．

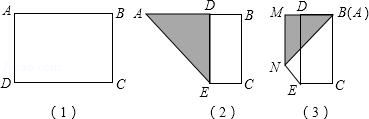
有一张长方形纸片ABCD，如图（1），将它折叠，使AD边落在AB边上，折痕为AE，如图（2）；再将∠A折叠，使点A与点B重合，折痕为MN，如图（3）．如果AD=4cm，MD=1cm，那么DB=      cm．

如图所示，折叠长方形ABCD的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，求EF的长．

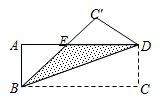
如图，把一张矩形纸片ABCD沿对角线BD折叠，使C点落在C'，且BC'与AD交于E点，若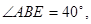则         °

内角和等于外角和2倍的多边形是     边形．

如图，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为P₁，第2次碰到矩形的边时的点为P₂，…，第n次碰到矩形的边时的点为P_n，则点P₃的坐标是    ；点P₂₀₁₄的坐标是     ．

如图，如果边长为1的等边△PQR沿着边长为1的正方形ABCD的外部的边如图位置开始顺时针连续滚动，当它滚动121次时，点P所经过的路程是_________．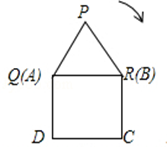

如图，在周长为20cm的平行四边形ABCD中，AB≠AD，对角线AC、BD相交于点O，OE⊥BD交AD于E，则△ABE的周长为          cm．

如图，在四边形ABCD中，AB∥CD，要使得四边形ABCD是平行四边形，应添加的条件是                 ．（只填写一个条件，不另外添加字母和线段）

一个多边形的每一个外角都等于36°，则该多边形的内角和等于      度．

如图，小明从A点出发前进10m，向右转15°，再前进10 m，又向右转15°，…，这样一直走下去，他第一次[回到出发点A时，一共走了      m。

如果一个正多边形的内角和是1440°，则这个正多边形是正边形。

如图1，正方形纸片ABCD的边长为2，翻折∠B、∠D，使得两个直角的顶点重合于对角线BD上一点P，EF、GH分别是折痕（如图2）．设AE＝x（0＜x＜2），给出下列判断：

①当x＝1时，点P是正方形ABCD的中心；
②当x＝时，EF＋GH＞AC；
③当0＜x＜2时，六边形AEFCHG面积的最大值是；
④当0＜x＜2时，六边形AEFCHG周长的值不变．
其中正确的是________（填序号）．

将矩形纸片ABCD按如图方式折叠，DE、CF为折痕，折叠后点A和点B都落在点O处．若△EOF是等边三角形，则的值为               ．