初中数学圆内接四边形的性质解答题

(Ⅰ)某服装厂承揽一项生产夏凉小衫1600件的任务，计划用 $t$天完成．
（1）写出每天生产夏凉小衫 $w$（件）与生产时间 $t$（天）（ $t>4$）之间的函数关系式;
（2）由于气温提前升高，商家与服装厂商议调整计划，决定提前4天交货，那么服装厂每天要多做多少件夏凉小衫才能完成任务？
(Ⅱ)如图，已知矩形 $ABCD$中， $E$是 $AD$上的一点， $F$是 $AB$上的一点， $EF\perp EC$，且 $EF=EC$， $DE=4cm$，矩形 $ABCD$的周长为32cm，求 $AE$的长．

如图，在▱ABCD中，E，F分别是BC，AD中点．
（1）求证：△ABE≌△CDF；
（2）当BC=2AB=4，且△ABE的面积为，求证：四边形AECF是菱形．

已知：平行四边形ABCD中，过对角线AC中点O的直线EF交AD于F，BC于E。
求证：BE=DF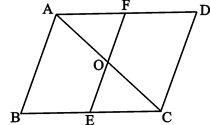

如图①，在矩形ABCD中，将矩形折叠，使B落在边AD（含端点）上，落点记为E，这时折痕与边BC或者边CD（含端点）交于F，然后展开铺平，则以B、E、F为顶点的三角形△BEF称为矩形ABCD的“折痕三角形”
（1）由“折痕三角形”的定义可知，矩形ABCD的任意一个“折痕△BEF”是一个　　三角形
（2）如图②、在矩形ABCD中，AB=2，BC=4，，当它的“折痕△BEF”的顶点E位于AD的中点时，画出这个“折痕△BEF”，并求出点F的坐标；
（3）如图③，在矩形ABCD中，AB=2，BC=4，该矩形是否存在面积最大的“折痕△BEF”？若存在，说明理由，并求出此时点E的坐标？若不存在，为什么？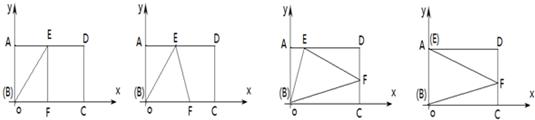

在正方形ABCD中，点G是BC上任意一点，连接AG，过B，D两点分别作BE⊥AG，DF⊥AG，垂足分别为E，F两点，求证：△ADF≌△BAE．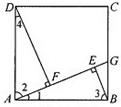

已知，E、F是四边形ABCD的对角线AC上的两点，AE=CF，BE=DF，BE∥DF．求证：四边形A BCD是平行四边形．

如图，已知四边形ABCD是平行四边形．
（1）求证：△MEF∽△MBA；
（2）若AF、BE分别是∠DAB，∠CBA的平分线，求证：DF=EC．

如图，在菱形ABCD中，∠A=60°，点P、Q分别在边AB、BC上，且AP=BQ．
（1）求证：△BDQ≌△ADP；
（2）已知AD=3，AP=2，求cos∠BPQ的值（结果保留根号）．

如图，在正方形ABCD中，E是AB边上任意一点，BG⊥CE，垂足为点O,交AC于点F，交AD于点G。
（1）证明：BE="AG" ；
（2）点E位于什么位置时，∠AEF=∠CEB，说明理由。

如图，在梯形ABCD中，AD∥BC,BC=2AD,点F、G分别是边BC、CD的中点，连接AF、FG，过点D作DE∥FG交AF于点E。
（1）求证：△AED≌△CGF；
（2）若梯形ABCD为直角梯形，∠B=90°，判断四边形DEFG是什么特殊四边形？并证明你的结论；
（3）若梯形ABCD的面积为a(平方单位），则四边形DEFG的面积为      （平方单位）。（只写结果，不必说理）

（11·曲靖）如图，在梯形ABCD中，AD∥BC，E、F分别是两腰AB、
DC的中点，AF、BC的延长线交于点G．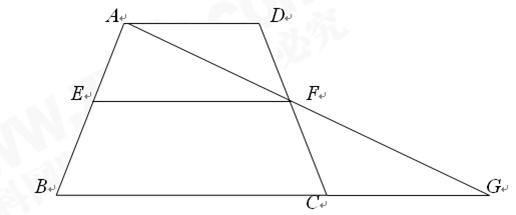

(1) 求证：△ADF≌△GCF．
(2) 类比三角形中位线的定义，我们把EF叫做梯形ABCD的中位线．阅读填空：
在△ABG中：∵E中AB的中点
由（1）的结论可知F是AG的中点，
∴EF是△ABG的_______线

因此，可将梯形中位线EF与两底AD，BC的数量关系用文字语言表述为______________．

（11·兵团维吾尔）如图，在等腰梯形ABCD中，AD＝4，BC＝9，∠
B＝45°．动点P从点B出发沿BC向点C运动，动点Q同时以相同速度从点C出发沿CD
向点D运动，其中一个动点到达端点时，另一个动点也随之停止运动．
（1）求AB的长；
（2）设BP＝x，问当x为何值时△PCQ的面积最大，并求出最大值；
（3）探究：在AB边上是否存在点M，使得四边形PCQM为菱形？请说明理由．

（11·兵团维吾尔）请判断下列命题是否正确？如果正确，请给出证明；
如果不正确，请举出反例．
（1）一组对边平行且相等的四边形是平行四边形；
（2）一组对角相等，一条对角线被另一条对角线平分的四边形是平行四边形．

如图，已知△ABC和△DEF是两个边长都为10cm的等边三角形，且B、D、C、E都在同一条直线上，连接AD、CF．

（1）求证：四边形ADFC是平行四边形；
（2）若BD=3cm，△ABC沿着BE的方向以每秒1cm的速度运动，设△ABC运动的时间为t秒，
①当t为何值时，平行四边形ADFC是菱形?请说明理由；
②平行四边形ADFC有可能是矩形吗?若可能，求出t的值；若不可能，请说明理由。

如图，已知点D在△ABC的BC边上，DE//AC交AB于E，DF//AB交AC于F．

（1）求证：AE=DF；
（2）若添加条件_______，则四边形AEDF是矩形；
若添加条件_______，则四边形AEDF是菱形；
若添加条件_______，则四边形AEDF是正方形．