初中数学圆内接四边形的性质解答题

已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平
分∠BCD，DF∥AB，BF的延长线交DC于点E．
求证△BFC≌△DFC；
AD=DE．

如图，△中，，、分別是△两个外角的平分线．
求证：；
若，试说明四边形是菱形．

）如图，等腰梯形ABCD中，AB=4，CD=9，∠C=60°，动点P从点C出发沿CD方向向点D运动，动点Q同时以相同速度从点D出发沿DA方向向终点A运动，其中一个动点到达端点时，另一个动点也随之停止运动.

求AD的长；
设CP=x， △PDQ的面积为y,求y关于x的函数表达式， 并求自变量的取值范围
探究：在BC边上是否存在点M使得四边形PDQM是菱形？若存在，请找出点M，并求出BM的长；不存在，请说明理由.

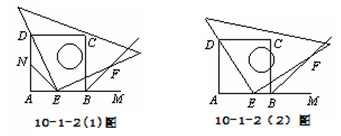
如图10－1－2（1），10－1－2（2），四边形ABCD是正方形，M是AB延长线上一点。直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A，B重合），另一条直角边与∠CBM的平分线BF相交于点F。
如图10－1－2（1），当点E在AB边的中点位置时：
①通过测量DE，EF的长度，猜想DE与EF满足的数量关系是         ；
②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是             ；
③请证明你的上述两猜想。
如图10－1－2（2），当点E在AB边上的任意位置时，请你在AD边上找到一点N，使得NE=BF，进而猜想此时DE与EF有怎样的数量关系。

如图1，AD∥BC，AB ⊥BC于B，∠DCB=75°，以CD为边的等边△DCE的另一顶点E在线段AB上．

(1)填空：∠ADE=____°；
(2)求证：  AB=BC;
(3)如图2所示，若F为线段CD上一点，∠FBC=30°，求的值．

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B.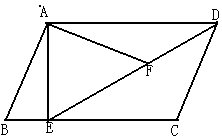

(1)求证：△ADF∽△DEC
(2)若AB＝4,AD＝3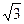,AE＝3,求AF的长.

(10分) 如图，Rt△ABC中，∠C = 90°，把Rt△ABC绕着B点逆时针旋转，得到Rt△DBE，点E在AB上．

（1）若∠BDA = 70°，求∠BAC的度数．
（2）若BC = 8，AC = 6，求△ABD中AD边上的高．

已知平行四边形ABCD中，对角线AC和BD相交于点O，AC=10，   
BD=8．
（1）若AC⊥BD，试求四边形ABCD的面积 ；
（2）若AC与BD的夹角∠AOD=，求四边形ABCD的面积；
（3）试讨论：若把题目中“平行四边形ABCD”改为“四边形ABCD”，且∠AOD= 
AC=，BD=，试求四边形ABCD的面积（用含，，的代数式表示）．

求证：矩形的对角线相等．