(10分) 如图，Rt△ABC中，∠C = 90°，把Rt△ABC绕着B点逆时针旋转，得到Rt△DBE，点E在AB上．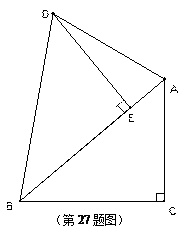
（1）若∠BDA = 70°，求∠BAC的度数．
（2）若BC = 8，AC = 6，求△ABD中AD边上的高．
，其中
．
；（2） 
相关知识点
推荐套卷
(10分) 如图，Rt△ABC中，∠C = 90°，把Rt△ABC绕着B点逆时针旋转，得到Rt△DBE，点E在AB上．
（1）若∠BDA = 70°，求∠BAC的度数．
（2）若BC = 8，AC = 6，求△ABD中AD边上的高．
粤公网安备 44130202000953号