初中数学圆内接四边形的性质选择题

如图，在直角三角形ABC中（∠C=90°），放置边长分别为3，4，x的三个正方形，则x的值为（ ）

A．5

B．6

C．7

D．12

将面积为a²的正方形边长增加2，则正方形的面积增加了（    ）

A．4

B．2a+4

C．4a+4

D．4a

如图，在Rt△ABC中，∠C=90°，AC=BC=6cm，点P从点A出发，沿AB方向以每秒cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动，将△PQC沿QC翻折，点P的对应点为点P′．设点Q运动的时间为t秒，若四边形QPCP′为菱形，则t的值为（ ）

A．

B．2

C．

D．3

如图 ，在矩形ABCD中 ，AB="10" ， BC="5" ．若点M、N分别是线段AC、AB上的两个动点，则BM+MN的最小值为（  ）          

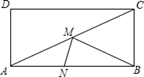
A．10        B． 8           C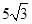．           D．6

下列条件之一能使菱形ABCD是正方形的为（ ）

①AC⊥BD  ②∠BAD=90°  ③AB=BC  ④AC=BD．
A.①③ B.②③ C.②④ D.①②③

已知平行四边形ABCD的对角线交于点O，则下列命题是假命题的是（ ）

A．若AC⊥BD，则平行四边形ABCD是菱形

B．若BO=2AO，则平行四边形ABCD是菱形

C．若AB=AD，则平行四边形ABCD是菱形

D．若∠ABD=∠CBD，则平行四边形ABCD是菱形

已知菱形的对角线分别长为6和8，则该菱形的周长为（  ）

A．5

B．15

C．20

D．24

如图，矩形ABCD中，AB=1，AD=2，M是CD的中点，点P在矩形的边上沿A→B→C→M运动，则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是（ ）

如图，以正方形ABCD的对角线AC为边作菱形AEFC，点E在边AB的延长线上，则∠FAE的度数为（   ）

A．15°

B．22.5°

C．30°

D．37.5°

下列命题是真命题的是（  ）

A．四边都相等的四边形是矩形

B．菱形的对角线相等

C．对角线互相垂直的四边形是正方形

D．对角线相等的菱形是正方形

如图，正方形ABCD的边长为4，P为正方形边上一动点，沿A→D→C→B→A 的路径匀速移动，设P点经过的路径长为x，△APD的面积是y，则下列图象能大致反映y与x的函数关系的是（ ）

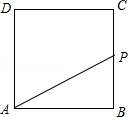
A．	B．
C．	D．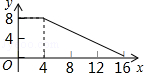

如图所示，在▱ABCD中，对角线AC，BD相交于点O，E，F是对角线AC上的两点，当E，F满足下列哪个条件时，四边形DEBF不一定是平行四边形（ ）

A．OE="OF"

B．DE="BF"

C．∠ADE="∠CBF"

D．∠ABE=∠CDF

顺次连接四边形ABCD四边中点得到新的四边形为菱形，那么原四边形ABCD为（  ）

A．矩形

B．菱形

C．对角线相等的四边形

D．对角线垂直的四边形

如图，在菱形ABCD中，AB=5，∠B=60°，则对角线AC的长等于（   ）

A．8

B．7

C．6

D．5

如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：
①BE=GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH
其中，正确的结论有（ ）

A．1个

B．2个

C．3个

D．4个