初中数学圆内接四边形的性质选择题

如图，在长为100m，宽为80 m的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7644m²，则道路的宽应为多少米？设道路的宽为x m，则可列方程为 （     ）

A．100×80－100x－80x="7644"	B．（100－x）（80－x）＋x^2="7644"
C．（100－x）（80－x）="7644"	D．100x＋80x－x^2=7644

如图所示，EF过矩形ABCD对角线的交点O，且分别交AB，CD于点E，F，若AB=3，BC=4，那么阴影部分的面积为（   ）

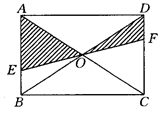
A．4

B．12

C．6

D．3

有一根长60cm的铁丝，用它围成一个矩形，写出矩形面积S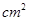（）与它的一边长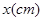之间的函数关系式为（   ）

A．

B．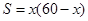

C．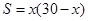

D．

一个多边形的内角和是外角和的2倍，则这个多边形是（      ）

A．四边形

B．五边形

C．六边形

D．八边形

一个正多边形的每个外角都是36°，这个正多边形的边数是（      ）

A．9

B．10

C．11

D．12

一个多边形截去一个角后，形成另一个多边形的内角和为720°，那么原多边形的边数为（  ）

A．5

B．5或6

C．5或7

D．5或6或7

已知四边形ABCD的两条对角线AC与BD互相垂直，则下列结论正确的是（ ）

A．当AC=BD时，四边形ABCD是矩形

B．当AB=AD，CB=CD时，四边形ABCD是菱形

C．当AB=AD=BC时，四边形ABCD是菱形

D．当AC=BD，AD=AB时，四边形ABCD是正方形

如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（ ）

A．78°

B．75°

C．60°

D．45°

如图，矩形纸片ABCD中，AB=6cm，BC=8cm，现将其沿AE对折，使得点B落在边AD上的点B₁处，折痕与边BC交于点E，则CE的长为（ ）

A．6cm

B．4cm

C．2cm

D．1cm

如图，矩形ABCD的对角线AC=8cm，∠AOD=120°，则AB的长为（ ）

A．cm

B．2cm

C．2cm

D．4cm

下列命题是假命题的是（ ）

A．四个角相等的四边形是矩形

B．对角线相等的平行四边形是矩形

C．对角线垂直的四边形是菱形

D．对角线垂直的平行四边形是菱形

如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC与点E，PF⊥CD于点F，连接EF，给出的下列结论：①AP=EF；②∠PFE=∠BAP；③PD=EC；④PB²+PD²=2PA²，正确的个数有（ ）

A．1

B．2

C．3

D．4

如图，菱形ABCD的周长为8cm，高AE长为cm，则对角线AC长和BD长之比为（ ）

A．1：2

B．1：3

C．1：

D．1：

在四边形ABCD中，AB∥DC，AD∥BC，如果添加一个条件，即可推出该四边形是矩形，那么这个条件可以是（ ）

A．∠D="90°"

B．OH="4"

C．AD="BC"

D．Rt△AHB

正方形ABCD内一点P，BP=2，把△ABP绕点B顺时针旋转90°得到△CBP′，则PP′的长为（ ）

A．2

B．2

C．3

D．3