河北省秦皇岛卢龙八年级上学期期中考试数学试卷
下面各组线段中,能组成三角形的是( )
| A.1,2,3 | B.1,2,4 | C.3,4,5 | D.4,4,8 |
到三角形的三个顶点距离相等的点是( )
| A.三条角平分线的交点 |
| B.三条中线的交点 |
| C.三条高的交点 |
| D.三条边的垂直平分线的交点 |
一个正多边形的每个外角都是36°,这个正多边形的边数是( )
| A.9 | B.10 | C.11 | D.12 |
一个多边形的内角和是外角和的2倍,则这个多边形是( )
| A.四边形 | B.五边形 | C.六边形 | D.八边形 |
下列关于全等三角形的说法不正确的是( )
| A.全等三角形的大小相等 |
| B.两个等边三角形一定是全等三角形 |
| C.全等三角形的形状相同 |
| D.全等三角形的对应边相等 |
如图,∠CAB=∠DBA,再添加一个条件,不一定能判△ABC≌△BAD的是( )

| A.AC=BD |
| B.AD=BC |
| C.∠DAB=∠CBA |
| D.∠C=∠D |
小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃.应该带( )

| A.第1块 | B.第2块 | C.第3块 | D.第4块 |
墨墨发现从某多边形的一个顶点出发,可以作4条对角线,则这个多边形的内角和是( )
| A.1260° | B.1080° | C.900° | D.720° |
点P(1,2)关于y轴对称点的坐标是( ).
| A.(-1,2) | B.(1,-2) | C.(1,2) | D.(-1,-2) |
如图,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交边AC点E,AC的长为12cm,则△BCE的周长等于( )

| A.16cm | B.20cm | C.24cm | D.26cm |
如图所示,∠A+∠B+∠C+∠D+∠E的结果为( )
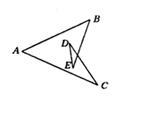
| A.90° | B.180° | C.360° | D.无法确定 |
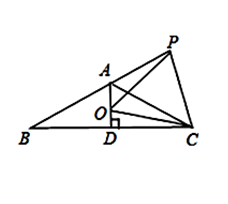
如图,等腰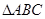 ,
,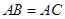 ,
,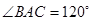 ,
,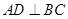 于点
于点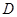 ,点
,点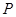 是
是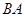 延长线上一点,点
延长线上一点,点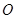 是线段
是线段 上一点,
上一点,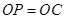 ,下面结论:
,下面结论:
①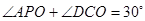 ;
;
②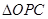 是等边三角形;
是等边三角形;
③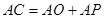 ;
;
④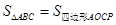 .
.
其中正确的是( ).
| A.②③ | B.①②④ | C.③④ | D.①②③④ |
已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 条.
如图,把两条钢条的中点连在一起,可以做成一个测量工件槽宽的工具(卡钳)。那么要测量工件内槽宽A'B',则只要测量AB即可。
1.卡钳的工作原理利用了三角形全等判定定理________________.
2.请说明这样测量的理由.
如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
作图题:
(1)利用网格线作图(充分利用格线或格点,完成如下操作):在BC上找一点P,使点P到AB和AC的距离相等.然后,在射线AP上找一点Q,使QB=QC
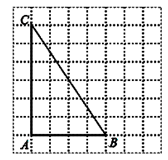
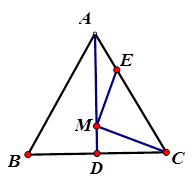
(2)如图,等边△ABC,AD是BC边上的中线,M是AD上的动点,E是AC边上一点
①作点E关于直线AD的对称点点E′;
②当EM+CM的值最小时,作出此时点M的位置(标注为M′)
如图,已知AD平分∠BAC交BC于D,DE⊥AB,DF⊥AC,垂足分别是E、F,求证:AD垂直平分EF.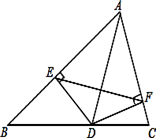
如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB垂足分别是E、F,求证:CE=DF
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的数量关系?请说明理由。
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:__________________________________。
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:__________________________________。 




 粤公网安备 44130202000953号
粤公网安备 44130202000953号