初中数学圆内接四边形的性质选择题

矩形ABCD中，边长AB=4，边BC=2，M、N分别是边BC、CD上的两个动点，且始终保持AM⊥MN．则CN的最大为（ ）

A．1           B．       C．      D．2

如图，正方形ABCD的边长为3，点E，F分别在边AB、BC上，AE=BF=1，小球P从点E出发沿直线EF向点F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当小球P第一次碰到点E时，小球P所经过的路程长为（ ）

A．12           B．9             C．4          D．6 

如图，四边形ABCD中，AC＝a，BD＝b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A₁B₁C₁D₁，再顺次连接四边形A₁B₁C₁D₁各边中点，得到四边形A₂B₂C₂D₂，如此进行下去，得到四边形A_nB_nC_nD_n．
①四边形A₄B₄C₄D₄是菱形；
②四边形A₃B₃C₃D₃是矩形；
③四边形A₇B₇C₇D₇周长为；
④四边形A_nB_nC_nD_n面积为．
上述结论正确的是（     ）

A．①②③

B．②③④

C．①③④

D．①②③④

如图，在矩形ABCD中，动点P从点B出发，沿BC、CD、DA运动至点A停止，设点P运动的路程为x，△ABP的面积为y，如果y关于x的函数图象如图所示，则△ABC的面积是 （    ）

A．20             B．18             C．16             D．10

如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：
①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH=BD；其中正确结论的是（   ）

A．①②③

B．①②④

C．①③④

D．②③④

如图，已知直线l₁∥l₂∥l₃∥l₄∥l₅，相邻两条平行直线间的距离相等且为1，如果四边形ABCD的四个顶点在平行直线上，∠BAD=90°且AB=3AD，DC⊥l₄，则四边形ABCD的面积是（   ）

A．9

B．14

C．

D．

如图，Rt△ABC中，∠C=90°，AC=3，BC=4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC，四块阴影部分的面积分别为S₁、S₂、S₃、S₄．则S₁+S₂+S₃+S₄等于（ ）

A．14         B．16           C．18        D．20

如图，已知在正方形ABCD中，点O为对角线AC的中点，过O点的射线OM、ON分别交AB、BC于点E、F，且∠EOF=90°，BO、EF交于点P，则下面结论中：①图形中全等的三角形只有三对；②△EOF是等腰直角三角形；③正方形ABCD的面积等于四边形OEBF面积的4倍；④BE+BF=OA；⑤+
=2OP·OB.正确结论的个数是（    ）

A.4个      B.3个        C.2个       D.1个

如图，在平面直角坐标系中，A(1,0)，B(0,3)，以AB为边在第一象限作正方形ABCD,点D在双曲线y=(k≠0)上，将正方形沿x轴负方向平移 m个单位长度后，点C恰好落在双曲线上，则m的值是                      （   ）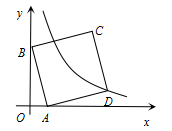

A．2

B．3

C．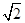

D．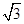

如图，将矩形纸片ABCD的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH，若EH=3，EF=4，则边AD的长是（）

A．2

B．3

C．4．8

D．5

如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（  ）

A．（60°，4）

B．（45°，4）

C．（60°，）

D．（50°，）

如图，E是边长为l的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值为（   ）

A．

B．

C．

D．

下列图形都是由同样大小的矩形按一定规律组成，其中第（1）个图形的面积为2，第（2）个图形的面积为8，第（3）个图形的面积为18，……，则第（10）个图形的面积为（    ）

A．196

B．200

C．216

D．256

如图，已知四边形ABCD为等腰梯形，AD∥BC，AB=CD，AD=，E为CD中点，连接AE，且AE=2，∠DAE=30°，作AE⊥AF交BC于F，则BF=（  ）

A．

B．

C．

D．

如图，已知正方形ABCD，点E是边AB的中点，点O是线段AE上的一个动点（不与A、E重合），以O为圆心，OB为半径的圆与边AD相交于点M，过点M作⊙O的切线交DC于点N，连接OM、ON、BM、BN．记△MNO、△AOM、△DMN的面积分别为S₁、S₂、S₃，则下列结论不一定成立的是（  ）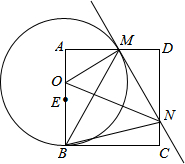

A．S₁＞S₂+S₃      B．△AOM∽△DMN      C．∠MBN=45°      D．MN=AM+CN