重庆市江津区四校九年级上学期期中联考数学试卷
已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( ) 
| A.45° | B.35° | C.25° | D.20° |
生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件.如果全组有x名学生,则根据题意列出的方程是( )
A. |
B. |
C. |
D. |
二次函数 的开口方向、对称轴、顶点坐标分别是( )
的开口方向、对称轴、顶点坐标分别是( )
A.向下、直线x= 、( 、( ,5) ,5) |
B.向上、直线x= 、( 、( ,5) ,5) |
C.向上、直线x=4、(4, ) ) |
| D.向上、直线x=4、(4,5) |
实数x满足方程(x2+x)2-(x2+x)-2=0,则x2+x的值等于( )
| A.2 | B. |
C.2或 |
D.1或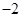 |
下列图形都是由同样大小的矩形按一定规律组成,其中第(1)个图形的面积为2 ,第(2)个图形的面积为8
,第(2)个图形的面积为8 ,第(3)个图形的面积为18
,第(3)个图形的面积为18 ,……,则第(10)个图形的面积为( )
,……,则第(10)个图形的面积为( )
A.196 |
B.200 |
C.216 |
D.256 |
二次函数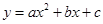 (
( )的图象如图所示,下列结论:(1)
)的图象如图所示,下列结论:(1)
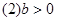 (3)
(3)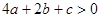 (4)
(4) 其中不正确的有( )
其中不正确的有( )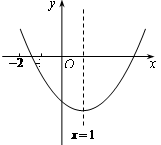
| A.1个 | B.2个 | C.3个 | D.4个 |
已知二次函数y=2x2-9x-34,当自变量x取两个不同的值x1,x2时,函数值相等,则当自变量x取x1+x2时的函数值应当与( )
| A.x=1时的函数值相等 |
| B.x=0时的函数值相等 |
C.x=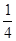 的函数值相等 的函数值相等 |
D.x= 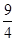 的函数值相等 的函数值相等 |
如图,在等腰Rt△ABC中,∠A=90°,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转90°得到线段OD,要使点D恰好落在BC边上,则OP的长等于 .
如图,二次函数y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C,则ac的值是 .
如图,在菱形ABCD中,AB=BD,点E、F分别在边AB,AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,若CG=4,则S四边形BCDG=_______________.
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.作出△ABC以O为旋转中心,顺时针旋转90°的△A1B1C1,(只画出图形).作出△ABC关于原点O成中心对称的△A2B2C2,(只画出图形),写出B2 和C2的坐标.
如图,抛物线 经过直线
经过直线 与坐标轴的两个交点A、B,此抛物线与
与坐标轴的两个交点A、B,此抛物线与 轴的另一个交点为C,抛物线顶点为D,
轴的另一个交点为C,抛物线顶点为D,
(1)求此抛物线的解析式;
(2)求四边形ADBC的面积;
(3)直接写出使 的x的取值范围.
的x的取值范围.
已知∠GOH=90°,A、C分别是OG、OH上的点,且OA=OC=4,以OA为边长作正方形OABC.现将正方形OABC绕O点顺时针旋转,当A点第一次落在∠GOH的角平分线OP上时停止旋转;旋转过程中,AB边交OP于点M,BC边交OH于点N(如图2),
(1)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
(2)设△MBN的周长为p,在正方形OABC的旋转过程中,p值是否有变化?请证明你的结论.
如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(2,0)和点B(-6,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与 轴交于点M ,在对称轴上存在点P,使△CMP为等腰三角形,请直接写出所有符合条件的点P的坐标.
轴交于点M ,在对称轴上存在点P,使△CMP为等腰三角形,请直接写出所有符合条件的点P的坐标.
(3)设点Q是抛物线对称轴上的一个动点,当点Q满足 最大时,求出Q点的坐标.
最大时,求出Q点的坐标.
(4)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
某电视机生产厂家去年销往农村的某品牌电视机每台的售价y(元)与月份x之间满足函数关系 ,去年的月销售量p(万台)与月份x之间成一次函数关系,其中两个月的销售情况如下表:
,去年的月销售量p(万台)与月份x之间成一次函数关系,其中两个月的销售情况如下表:
(1)求p与x之间的一次函数关系.
(2)求该品牌电视机在去年哪个月销往农村的销售金额最大?最大是多少?
(3)由于受国际金融危机的影响,今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了 ,且每月的销售量都比去年12月份下降了
,且每月的销售量都比去年12月份下降了 。国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予财政补贴。受此政策的影响,今年3月份至5月份,该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台。若今年3至5月份国家对这种电视机的销售共给予财政补贴936万元,求
。国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予财政补贴。受此政策的影响,今年3月份至5月份,该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台。若今年3至5月份国家对这种电视机的销售共给予财政补贴936万元,求 的值(保留一位小数)
的值(保留一位小数)
(参考数据: ,
, ,
, ,
, 销售金额=售价
销售金额=售价 销售量)
销售量)
 的一元二次方程的是( )
的一元二次方程的是( )



 的根是( )
的根是( )




 的图象经过原点,则
的图象经过原点,则 的值为( )
的值为( ) 的值一定是( )
的值一定是( ) 的一般形式是 .
的一般形式是 . 是方程
是方程 的一个根,则代数式
的一个根,则代数式 =__________.
=__________.
 -4)÷
-4)÷ ,其中x是方程
,其中x是方程 的根.
的根. 的两个根,求△ABC的周长.
的两个根,求△ABC的周长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号