如图□ABCD中,∠ABC和∠BCD的平分线交AD于同一点E,BE = 4,CE = 3,AB长是( )

A. |
B.3 | C.4 | D.5 |
如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是( )

如图,在矩形ABCD中,AB=6,BC=8,现要在该矩形中作出面积最大的菱形,则菱形的边长为( )
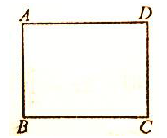
| A.5 | B.6 | C. |
D. |
如图,以正方形ABCD的对角线AC为边作菱形AEFC,点E在边AB的延长线上,则∠FAE的度数为( )

| A.15° | B.22.5° | C.30° | D.37.5° |
如图,在菱形ABCD中,AB=5,∠B=60°,则对角线AC的长等于( )

| A.8 | B.7 | C.6 | D.5 |
长方形ABCD中,AD="4" cm,AB="10" cm,按右图方式折叠,使点B与点D重合,折痕是EF,则DE等于 ( )

| A.4.2 cm | B.5.8 cm | C.4.2 cm或5.8 cm | D.6 cm |
如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α等于( ).
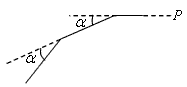
| A.30° | B.40° | C.80° | D.不存在 |
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°, ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )

A. |
B.2 | C.3 | D. |
如图,在3×3的正方形网格中,则∠1+∠2+∠3+∠4+∠5等于 ( ).

| A.180° | B.225° | C.270° | D.315° |
如图,将长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,那么∠DAE等于( ).
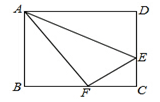
| A.60° | B.45° | C.30° | D.15° |
下列说法中,正确的是( )
| A.同位角相等 |
| B.对角线相等的四边形是平行四边形 |
| C.四条边相等的四边形是菱形 |
| D.矩形的对角线一定互相垂直 |
如图(a),直角梯形ABCD,∠B=90°,DC∥AB,动点P从B点出发,以每秒2个单位长度,由B-C-D-A沿边运动,设点P运动的时间为x秒,△PAB的面积为y,如果关于x的函数y的图象如图(b),则函数y的最大值为( )

| A.18 | B.32 | C.48 | D.72 |
如图,把长方形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:
①△EBD是等腰三角形,EB="ED" ;
②折叠后∠ABE和∠CBD一定相等;
③折叠后得到的图形是轴对称图形;
④△EBA和△EDC一定是全等三角形.
其中正确的有( )

| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在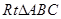 中,
中,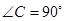 ,
,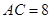 ,
,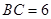 ,点
,点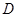 是
是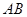 上的一个动点(不与
上的一个动点(不与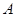 、
、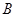 两点重合),
两点重合),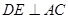 于点
于点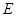 ,
,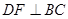 于点
于点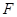 ,点
,点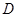 从靠近点
从靠近点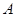 的某一点向点
的某一点向点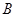 移动,矩形
移动,矩形 的周长变化情况是( )
的周长变化情况是( )
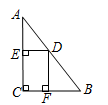
| A.逐渐减小 | B.逐渐增大 | C.先增大后减小 | D.先减小后增大 |