已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,
问题1:如图1,P为AB边上的一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
问题2:如图2,若P为AB边上一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题3:若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题4:如图3,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作平行四边形PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
如图.在△ABC中.D是AB的中点.E是CD的中点.过点C作CF∥AB交AE的延长线于点F.连结BF。
(1)求证:DB=CF;
(2)在△ABC中添加一个条件: ,使四边形BDCF为 (填:矩形或菱形)。
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为100,小正方形的面积为4,若用x,y表示直角三角形的两直角边(x>y),下列4个说法:
① ;②x-y=2;③
;②x-y=2;③ ;④x+y="14." 其中说法正确的是 (只填序号)
;④x+y="14." 其中说法正确的是 (只填序号)
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使得△AMN周长最小时,则∠AMN+∠ANM的度数为( )
A.100° B.110° C.120° D.130°

已知:在四边形ABCD中,AC = BD,AC与BD交于点O,∠DOC = 60°.
(1)当四边形ABCD是平行四边形时(如图1),证明AB + CD = AC;
(2)当四边形ABCD是梯形时(如图2),AB∥CD,线段AB、CD和线段AC之间的数量关系是_____________________________;
(3)如图3,四边形ABCD中,AB与CD不平行,结论AB + CD = AC是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
如图,将一张矩形纸片 沿EF折叠,使点
沿EF折叠,使点 落在
落在 边上的点B处;沿BG折叠,使点
边上的点B处;沿BG折叠,使点 落在点D处,且BD过F点.
落在点D处,且BD过F点.
⑴试判断四边形BEFG的形状,并证明你的结论.
⑵当∠BFE为多少度时,四边形BEFG是菱形.
如图,网格中每一个小正方形的边长为1个单位长度.
⑴AB的长度为 .
⑵请在所给的网格内画出以线段AB为腰、BC为下底的等腰梯形ABCD;
⑶梯形ABCD的面积等于_________.
在课外活动课上,老师让同学们做一个对角线互相垂直的等腰梯形形状的风筝,其面积为450cm2,则对角线所用的竹条至少需 cm
下列命题正确的是
| A.同一边上两个角相等的梯形是等腰梯形; |
| B.一组对边平行,一组对边相等的四边形是平行四边形; |
| C.如果顺次连结一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方形。 |
| D.对角线互相垂直的四边形面积等于对角线乘积的一半。 |
如图,把菱形ABCD沿AH折叠,使B点落在BC上的E点处,若∠B=700,则∠EDC的大小为
| A.100 | B.150 | C.200 | D.300 |
如图,□ABCD的对角线AC、BD相交于O,EF过点O与AD、BC分别相交于E、F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A、16 B、14 C、12 D、10
用两个全等的等边三角形,可以拼成下列哪种图形( )
| A.矩形 | B.菱形 | C.正方形 | D.等腰梯形 |
(1)四年一度的国际数学家大会于2002年8月20日在北京召开,大会会标如下图1,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和是5,求中间小正方形的面积.
(2)(2)现有一张长为6.5cm,宽为2cm的纸片,如图9,请你将它分割成6块,再拼合成一个正方形.(要求:先在图2中画出分割线,再画出拼成的正方形并标明相应数据)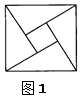
如图,四边形ABCD是菱形,对角线AC=8 cm , BD=6 cm, DH⊥AB于H,求:DH的长
如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果 ,则
,则 等于( )
等于( )
A. |
B. |
C. |
D.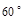 |
