初中数学圆试题

如图，网格中每一个小正方形的边长为１个单位长度．
AB的长度为        .
请在所给的网格内画出以线段AB为腰、BC为下底的
等腰梯形ABCD；
梯形ABCD的面积等于_________．

设长方形的长a=2，宽b=3，则面积S=________．

已知：在四边形ABCD中，AC = BD，AC与BD交于点O，∠DOC = 60°.
当四边形ABCD是平行四边形时（如图1），证明AB + CD = AC；
当四边形ABCD是梯形时（如图2），AB∥CD，线段AB、CD和线段AC之间的数量关系是_____________________________；
如图3，四边形ABCD中，AB与CD不平行，结论AB + CD = AC是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由.

如图，网格中每一个小正方形的边长为１个单位长度．
AB的长度为        .
请在所给的网格内画出以线段AB为腰、BC为下底的
等腰梯形ABCD；
梯形ABCD的面积等于_________．

在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN⊥DM，垂足为M，交∠CBE的平分线于点N .
写出点C的坐标；
求证：MD = MN；
连接DN交BC于点F，连接FM，下列两个结论：①FM的长度不变；②MN平分∠FMB，其中只有一个结论是正确的，请你指出正确的结论，并给出证明.

如图，将一张矩形纸片沿EF折叠，使点落在 边上的点B处；沿BG折叠，使点落在点D处，且BD过F点.
试判断四边形BEFG的形状，并证明你的结论.
当∠BFE为多少度时，四边形BEFG是菱形.

在课外活动课上，老师让同学们做一个对角线互相垂直的等腰梯形形状的风筝，其面积为450cm²，则对角线所用的竹条至少需        cm

下列命题正确的是

A．同一边上两个角相等的梯形是等腰梯形；

B．一组对边平行，一组对边相等的四边形是平行四边形；

C．如果顺次连结一个四边形各边中点得到的是一个正方形，那么原四边形一定是正方形。

D．对角线互相垂直的四边形面积等于对角线乘积的一半。

如图，把菱形ABCD沿AH折叠，使B点落在BC上的E点处，若∠B=70⁰，则∠EDC的大小为

A．10^0

B．15^0

C．20^0

D．30^0

如图，□ABCD的对角线AC、BD相交于O，EF过点O与AD、BC分别相交于E、F，若AB=4，BC=5，OE=1.5,那么四边形EFCD的周长为（ ）
A、16               B、14               C、12              D、10

用两个全等的等边三角形，可以拼成下列哪种图形（ ）

A．矩形

B．菱形

C．正方形

D．等腰梯形

如图，四边形ABCD是菱形，对角线AC＝8 cm , BD＝6  cm,  DH⊥AB于H，求：DH的长

如图,矩形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果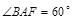 等于(  )                                                            

A．

B．

C．

D．

顺次连结等腰梯形各边中点所得的四边形一定是（ ）

A．菱形

B．矩形

C．梯形

D．正方形

在△ABC中(1)若∠A=60°，AB、AC边上的高CE、BD交于点O。求∠BOC的度数。

(2)若∠A为钝角，AB、AC边上的高CE、BD所在直线交于点O，画出图形，并用量角器量一量∠BAC+∠BOC=______°，再用你已学过的数学知识加以说明。
(3)由(1)(2)可以得到，无论∠A为锐角还是钝角，总有∠BAC+∠BOC=____°。